【华泰金工林晓明团队】从关联到逻辑：因果推断初探——华泰人工智能系列之三十

来源：华泰金融工程

林晓明    S0570516010001    研究员

陈   烨    S0570518080004    研究员

李子钰    S0570519110003    研究员

何康       S0570118080081    联系人

王晨宇    S0570119110038    联系人

报告发布时间：2020年4月24日

摘要

本文介绍了因果推断的框架，并研究了股票所属概念和收益的因果关系

人工智能领域中，机器学习的优势在于强大的关联挖掘能力，然而由于缺乏逻辑推理能力，机器学习无法区分数据中的因果关联和虚假关联。因果推断是用于解释分析的建模工具，可帮助恢复数据中的因果关联，有望实现可解释的稳定预测。本文介绍了基于倾向性评分法的因果推断框架，归纳了三个关键步骤，并分别在Lalonde数据集和A股概念数据中进行因果效应估计。结果显示，2016年以来在中证800成分股中，基金重仓(季调)概念与股票未来一个月收益有正向因果关系，股票质押概念与股票未来一个月收益有反向因果关系，预增和护城河概念与股票收益的因果效应存疑。

机器学习本质是曲线拟合，可借助因果推断构建稳健、有推理能力的AI

现有的大部分机器学习模型是关联驱动的，本质上是曲线拟合。关联主要有三个来源：因果关联，选择性偏差和混杂偏倚。其中选择性偏差和混杂偏倚产生的关联是不稳定的。因果推断可以帮助恢复数据中的因果关联，用于指导机器学习，实现可解释的稳定预测。对于金融市场来说，一方面市场环境持续变化的特性导致多种可观测因素的有效性都随之而变；另一方面，资产管理人对策略内部的因果逻辑和可解释性都有较高要求。这些现状都说明在将机器学习方法运用于金融市场的策略构建时，融入因果推断的方法是一个值得尝试的方向。

本文介绍了基于倾向性评分法的因果推断框架

因果推断的基本思想是在处理组和对照组间进行对照实验以估计因果效应。在观测数据中，将处理组与对照组之间分布不一样且会对结果造成影响的特征称为混淆变量，因果效应评估的关键是如何保证混淆变量在处理组与对照组的分布一致。倾向性评分法将多个混淆变量的影响用一个综合的倾向性评分来表示，降低了混淆变量的维度，使得控制混淆变量成为可能。本文归纳了倾向性评分法的三个步骤：(1)计算倾向性评分并估计因果效应；(2)评估各倾向性评分方法的均衡性；(3)通过反驳评估所估计的因果效应是否可靠。

基于倾向性评分法，本文研究股票所属概念和收益的因果关系

本文首先在经典的Lalonde数据集上进行因果效应估计。然后基于倾向性评分法，研究了中证800成分股中股票所属的四个概念和股票未来一个月收益的因果关系，我们选取的混淆变量为股票的基本面和量价因子暴露，考察区间为2016年1月到2020年3月。通过倾向性评分法的分析，我们认为基金重仓(季调)概念与股票收益有正向因果关系，股票质押概念与股票收益有反向因果关系，预增和护城河概念与股票收益的因果效应存疑。另外，倾向性评分加权法(PSW)在均衡性测试和反驳测试中表现都最好，可以认为其估计的因果效应较为可靠。

风险提示：因果推断所得结论是对历史规律的总结，若未来规律发生变化，结论存在失效的风险。倾向性评分法对于因果关系的建模存在过度简化的风险。倾向性评分法中，混淆变量的选取会对因果效应估计结果造成较大影响，应谨慎对待。

机器学习和因果推断

机器学习面临的风险

过去10年，以深度学习为代表的机器学习方法引领了人工智能的发展，在图像、语音、文本等多个领域中取得巨大成就。从根本上来说，机器学习是一种“连接主义”方法，即通过关联驱动的方式在大量的数据中进行拟合从而总结出规律。然而机器学习的工作方式离人脑依然有相当距离，不同于机器学习需要大量的数据，人类在学习过程中只需要比较少量的信息就能掌握规律，并通过逻辑推理不断适应事物和环境的变化。由于机器学习不具备逻辑推理的能力，无法区分数据中的因果关联和虚假关联，因而在数据匮乏或规律持续变化的环境中，机器学习模型难以展现出类似人脑的泛化性能。图灵奖得主、贝叶斯网络之父Judea Pearl认为现在人工智能的发展进入新的瓶颈期，大多数新的研究成果本质上是“曲线拟合”的工作。Pearl认为人们应该更关注人工智能中的因果推断(causal inference)，这可能是实现通用人工智能的必由之路。

我们将通过两个案例说明当前机器学习可能面临的风险。

首先以一个图像识别问题为例：识别一张图片中是否有狗。如图表1所示，如果训练集有选择性偏差，使得我们拿到的图片有80%都是草地上的狗，这样就会导致在训练集中草地这一特征会和图片中是否有狗这个标签十分相关。基于这样的有偏数据集学习到的预测模型，很有可能会将草地学习成很重要的特征，但显然这是不合理的，图片中的草地并不能决定是否有狗，真正决定图片中是否有狗的特征是狗的鼻子、耳朵、尾巴等等。对于测试集，如果跟训练集一样也是狗在草地上，则模型可以正确地预测；如果图片中的狗在有绿植的沙滩上，模型或许能识别出来；但是如果图片中的狗在水里，模型则大概率会识别不准。因此这样的模型对于未知测试集的预测效果并不稳定。

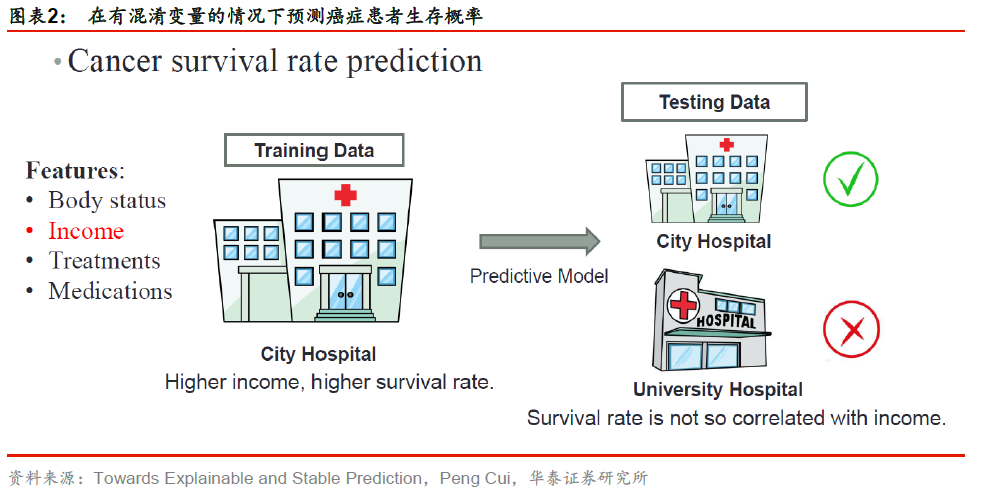
再举一个医疗领域的例子：预测一个癌症患者的生存率。假设我们拿到了某个城市某个医院的数据，基于该数据学习到的模型有可能会把患者的收入学习成很重要的特征。当然这也是有道理的，收入高的患者能负担得起更好的治疗，生存率也会越高。但是收入并不是患者生存率的决定因素，真正影响生存率的是患者接受的治疗水平以及患者本身的身体素质等因素，即使是收入很高的患者，如果没有接受很好的治疗，或者本身体质虚弱，免疫力低下，生存率依然会很低。利用该模型做预测时，如果未来要预测的患者同样来自该医院，我们可能会得到很准确的预测结果。但是如果要预测的患者来自大学校医院，由于校医院对患者给予的治疗不由收入决定，此时的预测结果很可能不准确。

机器学习模型表现不稳定的原因可能有以下两方面：

1.     一方面是数据的问题，现有的大部分机器学习方法都依赖于独立同分布(I.I.D)假设，即训练数据和测试数据是独立同分布的。在大数据条件下，由于训练数据可能已经涵盖了所有未来会出现的测试数据分布类型，这一假设或许能成立。然而在现实中，该假设很难满足，这样就会产生分布偏移(distribution shift)的问题。

2.     另一方面是模型的问题，现有的大部分机器学习模型是关联驱动的。关联主要有三个来源：Causation，Selection bias，Confounding bias。

(1)   Causation(因果关联)是不会随着环境和数据集的变化而变化的(比如下雨会导致地面湿，这在任何城市和国家都是成立的)，是稳定且可解释的。

(2)   Selection bias(选择性偏差)描述的就如图表1中草地和狗的例子，由于样本选择导致草地和狗十分相关，同样也可以通过样本选择使得沙滩等其它背景与狗十分相关，这种关联会随着数据集和环境的变化而变化。

(3)   Confounding bias(混杂偏倚)描述的是由于某些混淆变量导致的关联，如图表2中癌症患者生存率的例子，患者的收入就是一个混淆变量。混淆变量与预测目标和其他因子都有关，如果未处理好混淆变量，则会掩盖或歪曲真实的关联。

通过Selection bias和Confounding bias产生的关联是不稳定的，这两种相关性为虚假相关(Spurious Correlation)。传统机器学习预测不稳定的主要原因就在于其没有区分因果关联与虚假关联，而笼统地将所有关联都用于模型学习和预测。

因果推断是用于解释分析的建模工具，可以帮助恢复数据中的因果关联，用于指导机器学习，有望实现可解释的稳定预测。对于金融市场来说，一方面市场环境持续变化的特性导致多种可观测因素的有效性都随之而变；另一方面，资产管理人对策略内部的因果逻辑和可解释性都有较高要求。这些现状都说明在将机器学习方法在运用于金融市场的策略构建时，融入因果推断的方法是一个值得尝试的方向。

因果推断简介

在因果推断研究的漫长历史中，诞生了众多模型，如贝叶斯网络、do-calculus、因果图等等。本文将不对各个因果推断模型进行详细介绍，而是从最常用的Rubin Causal Model(RCM)出发，介绍因果推断的研究方法。

RCM模型

平均因果作用估计

最直接的平均因果作用估计方法为随机化实验。但随机化实验是有成本的，很多情况下会影响用户体验，甚至由于伦理道德等问题是不可行的，比如研究者不能因为想研究吸烟与肺癌的因果关系，就强迫受试者吸烟。因此常用的方法是使用观测数据估计因果效应。如图表3所示，在观测数据中，将处理组与对照组之间分布不一样且会对结果造成影响的特征称为Confounders(混淆变量)。当我们在研究Treatment变量T对Outcome变量Y的因果效应时，如果存在混淆变量W，它会影响Treatment变量T，也会影响最后的结果Y。当我们直接通过数据计算T对Y的关联时，实际上将W对Y的效应也计算在内，因此很难区分T对Y的关联是由T对Y的因果效应导致的，还是由混淆变量W通过T对Y产生影响导致的。

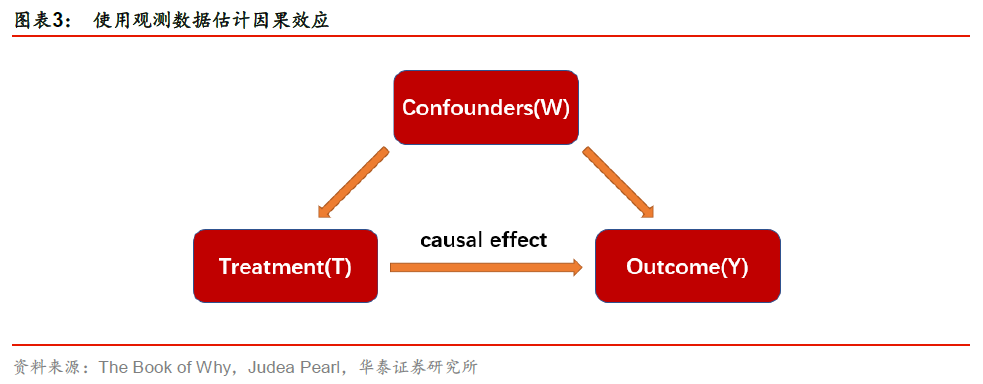
因此在基于观测数据进行因果效应评估时，关键是如何保证混淆变量在评估数据的处理组与对照组的分布是一致的。最直接的是基于匹配的方法，为处理组匹配对照组中特征分布一致的人群，通过匹配后的人群计算因果效应。但是在高维情况下很难找到两个特征分布完全一样的样本，因此该方法很难应用到高维情况中。为了解决这个问题，研究者们提出了基于倾向性评分(propensity score)的方法，本文将重点介绍该方法并给出实证案例。

基于倾向性评分法的因果推断

倾向性评分法由Rosenbaum和Rubin于1983年首次提出，是控制混淆变量的常用方法，其基本原理是将多个混淆变量的影响用一个综合的倾向性评分来表示，从而降低了混淆变量的维度。图表4展示了基于倾向性评分法的因果推断流程，主要包含三个关键步骤。本文将逐一进行详细说明。

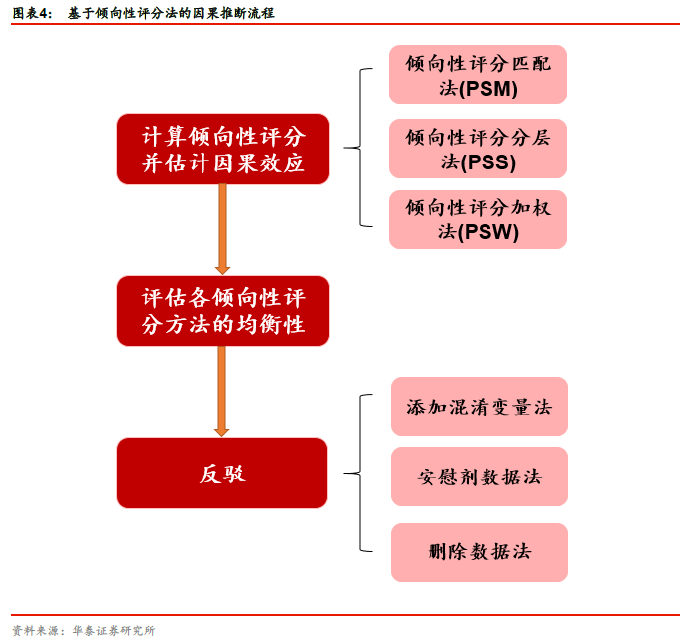
计算倾向性评分并估计因果效应

倾向性评分是给定混淆变量W的条件下，个体接受Treatment的概率估计，即 P(T=1|W)。如图表5所示，要计算每个研究对象的倾向性评分，需要以Treatment为因变量，混淆变量Confounders为自变量，建立回归模型(如Logistic回归)来估计每个研究对象接受Treatment的可能性。对于倾向性评分接近的样本，则认为它们近似匹配，可用来评估因果效应。匹配完成之后，即可通过下式计算Treatment变量T对Outcome变量Y的因果效应。

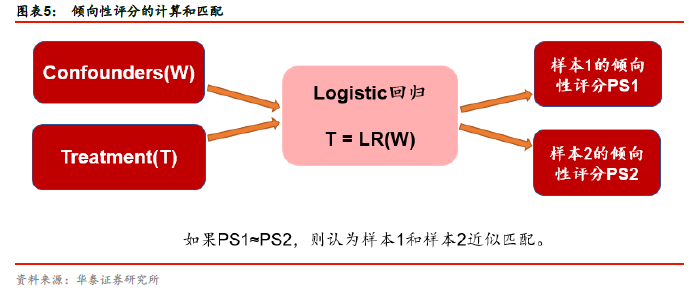
1.       倾向性评分匹配法(Propensity Score Matching，PSM)：PSM将处理组和对照组中倾向性评分接近的样本进行匹配后得到匹配群体，再在匹配群体中计算因果效应。最常用的匹配方法是最近邻匹配法(nearest neighbor matching)，对于每一个处理组的样本，从对照组选取与其倾向评分最接近的所有样本，并从中随机抽取一个或多个作为匹配对象，未匹配上的样本则舍去。

2.       倾向性评分分层法(Propensity Score Stratification，PSS)：PSS将所有样本按照倾向性评分大小分为若干层(通常分为5-10层)，此时层内组间混淆变量的分布可以认为是均衡的，当层内有足够样本量时，可以直接对单个层进行分析，也可以对各层效应进行加权平均。当两组的倾向性评分分布偏离较大时，可能有的层中只有对照组个体，而有的层只有试验组的个体，这些层不参与评估因果效应。PSS的关键问题是分层数和权重的设定。可通过比较层内组间倾向性评分的均衡性来检验所选定的层数是否合理，权重一般由各层样本占总样本量的比例来确定。有研究表明，采用五等分可以有效消除倾向分数模型中所有特征变量90%以上的偏差。(见参考文献[4])

倾向性评分加权法(Propensity Score Weighting，PSW)：PSW在计算得出倾向性评分的基础上，通过倾向性评分值赋予每个样本一个相应的权重进行加权，使得处理组和对照组中倾向性评分分布一致，从而达到消除混淆变量影响的目的。Robins等人给出的加权系数计算方法是：

以上两式中，PS是样本的倾向性评分。该加权方法的通俗理解方式为：由于PS是由Logistic回归拟合得到，总体上来看处理组样本的PS靠近1，对照组样本的PS靠近0。PS越小的处理组样本，越容易找到能与之匹配的对照组样本，使用该处理组样本估计的因果效应更可靠，其权重应该更大。所以对于处理组样本来说，其权重                                               等于PS的倒数。而对照组样本的情况和处理组样本正好相反，故其权重等于(1-PS)的倒数。

然而在大多数情况下，处理组和对照组样本的数量并不均衡。Hernan等人对计算方法进行了调整，将整个样本空间中处理组样本的占比()和非处理组样本的占比()加入公式中，增大占比较大组的样本的权重，得到以下计算方法：

在给样本加权后，即可计算因果效应。PSW的优点在于可以充分利用每个样本，不会出现样本无法匹配的情况。(见参考文献[5])

倾向性评分法的均衡性检验

倾向性评分法要求匹配后样本的所有混淆变量在处理组和对照组达到均衡，否则后续分析会有偏差，因此需要对匹配之后的样本进行均衡性检验。目前学术界比较公认的方法是使用标准化差值直观反映匹配前后的组间差异(见参考文献[6])。比如，混淆变量x的标准化差计算公式为

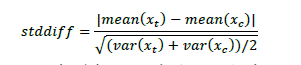
反驳

反驳(Refute)使用不同的数据干预方式进行检验，以验证倾向性评分法得出的因果效应的有效性。反驳的基本原理是，对原数据进行某种干预之后，对新的数据重新进行因果效应的估计。理论上，如果处理变量(Treatment)和结果变量(Outcome)之间确实存在因果效应，那么这种因果关系是不会随着环境或者数据的变化而变化的，即新的因果效应估计值与原估计值相差不大。

反驳中进行数据干预的方式有：

1.    安慰剂数据法：用安慰剂数据(Placebo)代替真实的处理变量，其中Placebo为随机生成的变量或者对原处理变量进行不放回随机抽样产生的变量。

2.    添加随机混淆变量法：增加一个随机生成的混淆变量。

3.     子集数据法：随机删除一部分数据，新的数据为原数据的一个随机子集。

因果推断程序包DoWhy简介

DoWhy(https://microsoft.github.io/dowhy/)是微软开发的用于因果推断的Python程序包。DoWhy通过简单的编程框架结合了若干因果推断方法。在DoWhy中可以使用的因果推断方法有：

1.       倾向性评分法(Propensity Score)。

2.       工具变量法(Instrument Variable)。

3.       断点回归法(Discontinuity Regression)。

我们将使用DoWhy中倾向性评分法相关的模块，展示因果推断在不同数据集上的应用案例。

因果推断程序包EconML简介

EconML (https://econml.azurewebsites.net/)同样是由微软开发的用于因果推断的Python程序包。相比DoWhy，EconML借助一些更复杂的机器学习算法来进行因果推断。在EconML中可以使用的因果推断方法有：

1.       双机器学习(Double Machine Learning)。

2.       双重鲁棒学习(Doubly Robust Learner)。

3.       树型学习器(Forest Learners)。

4.       元学习器(Meta Learners)。

5.       深度工具变量法(Deep IV).

6.       正交随机树(Orthogonal Random Forest)

7.       加权双机器学习(Weighted Double Machine Learning)

由于篇幅有限，本文将不对EconML做详细介绍。

基于倾向性评分法的因果推断案例：Lalonde数据集

Lalonde数据集是因果推断领域的经典数据集，由Robert Lalonde在1986年整理，数据集的说明如图表6所示：

数据集共包含445个观测对象，一个典型的因果推断案例是研究个人是否参加就业培训对1978年实际收入的影响。按照是否参加培训将所有观测对象进行分组，处理组(treat=1)185例，对照组(treat=0)260例。混淆变量为age、educ、black、hisp、married、nodeg。

第一步：使用倾向性评分法估计因果效应

各种倾向性评分法的因果效应估计值在图表7中，由于不同方法的原理不同，估计的因果效应值也不同。其中倾向性评分匹配法(PSM)因果效应估计值为2196.61，即参加职业培训可以使得一个人的收入增加约2196.61美元。另外为了对比，我们计算ATE(Average Treatment Effect)，即在不考虑任何混淆变量的情况下，参加职业培训(treat=1)和不参加职业培训(treat=0)两个群体收入(re78)的平均差异。

第二步：评估各倾向性评分方法的均衡性

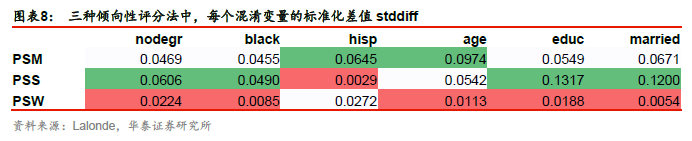
图表8展示了各倾向性评分方法中，每个混淆变量的标准化差值stddiff。总体来看，倾向性评分加权法(PSW)中各混淆变量的标准化差值最小(除了hisp)，说明PSW中混淆变量在处理组和对照组间较均衡，其因果效应估计值可能更可靠。

第三步：反驳

图表8展示了100次反驳测试中，三种倾向性评分法的每类反驳测试结果的均值。我们将三种倾向性评分法在真实数据下的因果效应估计值放在图表9最右侧进行对比。在安慰剂数据法中，由于生成的安慰剂数据(Placebo)替代了真实的处理变量，每个个体接收培训的事实已不存在，因此反驳测试中的因果估计效应大幅下降，接近0，这反过来说明了处理变量对结果变量具有一定因果效应。在添加随机混淆变量法和子集数据法中，反驳测试结果的均值在1585.19~1681.75之间。对比真实数据的因果估计效应值，PSM的反驳测试结果大符下降，说明其估计的因果效应不太可靠；PSW的反驳测试结果与真实数据因果效应估计值最接近，说明其因果效应估计值可能更可靠。

基于倾向性评分法的因果推断案例：A股概念数据

本章我们将把视角转回投资领域，分析A股市场中股票所属概念和股票未来收益的因果关系。股票是否属于某个概念是一种事件型的变量，可以套用到因果推断的框架中进行研究。本文使用的基于因果推断的方法，或许能为概念/事件驱动型策略提供一套科学的研究框架。

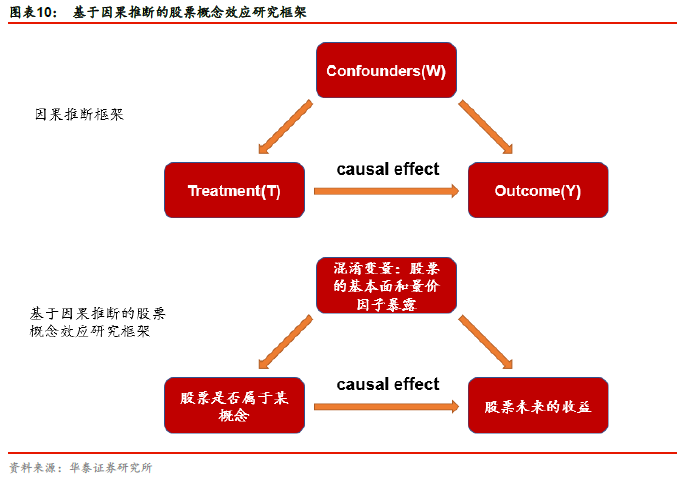
图表10展示了基于因果推断的股票概念效应研究框架。股票是否属于某概念(是=1，否=0)可视为处理变量(Treatment)，股票未来的收益可视为结果变量(Outcome)。股票的基本面的和量价因子暴露与股票未来收益有关，与股票的概念取值也可能有关，因此可视为混淆变量。我们要研究的是，控制混淆变量在处理组(属于某概念)和对照组(不属于某概念)的分布一致的情况下，股票所属概念和股票未来收益的因果关系。

本章的测试细节如下：

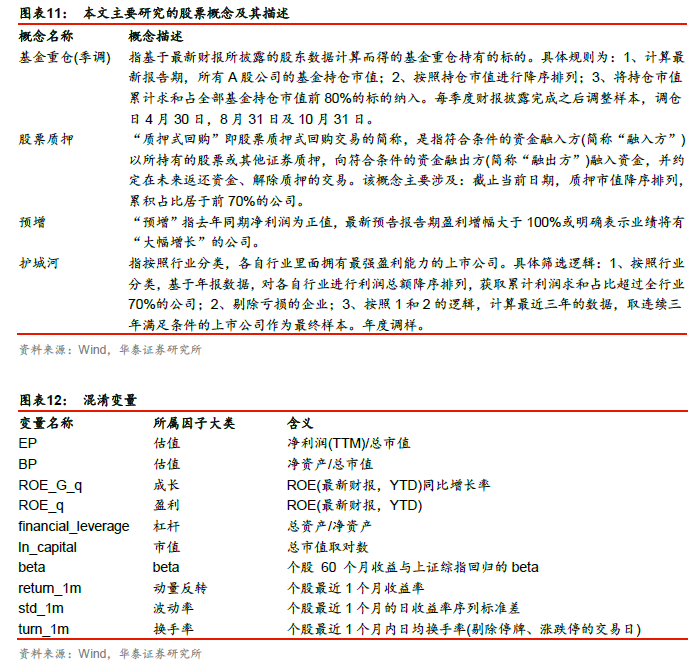
1.     处理变量：股票是否属于某概念。我们所使用的概念数据来自于Wind概念指数成分股，主要研究的股票概念如图表11所示。

2.     结果变量：为了方便不同截面月份进行对比，使用股票未来一个月的收益排序数(取值0~1之间，收益越高越大)作为结果变量。

3.     混淆变量：我们选取图表12中的因子作为混淆变量，混淆变量覆盖了各大类风格因子。

4.     样本空间：由于概念覆盖的股票数量有限，样本空间为中证800成分股。

时间区间：由于概念存在的时间较晚，时间区间为2016年1月至2020年3月。

基金重仓(季调)

图表13展示了每个月截面上中证800成分股中属于基金重仓(季调)概念的比例。

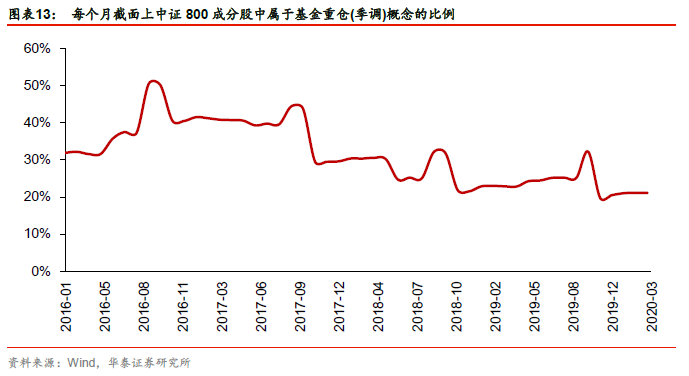
第一步：使用倾向性评分法估计因果效应

各种倾向性评分法的因果效应估计值在图表14中，其中倾向性评分匹配法(PSM)因果效应估计值为0.0388，即在2016年1月至2020年3月这段时间中，属于基金重仓(季调)概念的股票，其未来一个月收益的排序数相比于不属于该概念的股票要高出0.0388。另外为了对比，我们计算ATE，即在不考虑任何混淆变量的情况下，属于基金重仓(季调)概念的股票和不属于基金重仓(季调)概念的股票的平均差异。图表15展示了三种倾向性评分法的因果效应估计值变化。可以看出，我们所选取的混淆变量对于因果效应估计值的影响不大。

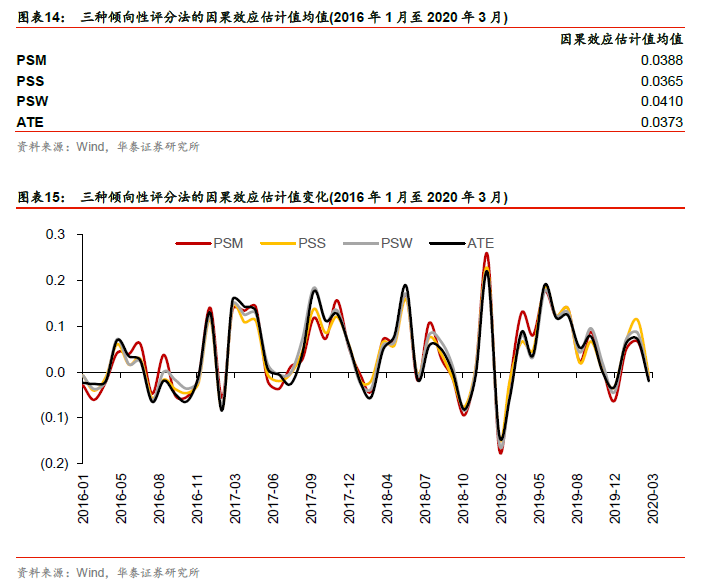
第二步：评估各倾向性评分方法的均衡性

图表16展示了各倾向性评分方法中，每个混淆变量的标准化差值stddiff。总体来看，倾向性评分加权法(PSW)中各混淆变量的标准化差值最小(除了ln_capital)，说明PSW中混淆变量在处理组和对照组间较均衡，其因果效应估计值可能更可靠。

第三步：反驳

图表17展示了100次反驳测试中，三种倾向性评分法的每类反驳测试结果的均值。我们将三种倾向性评分法在真实数据下的因果效应估计值放在图表17最右侧进行对比。在安慰剂数据法中，由于生成的安慰剂数据(Placebo)替代了真实的处理变量，每个样本是否属于概念的事实已不存在，因此反驳测试中的因果估计效应大幅下降，接近0，这反过来说明了处理变量对结果变量具有一定因果效应。在添加随机混淆变量法和子集数据法中，PSW的反驳测试结果与真实数据因果效应估计值最接近，说明其因果效应估计值可能更可靠。

股票质押

图表18展示了每个月截面上中证800成分股中属于股票质押概念的比例。

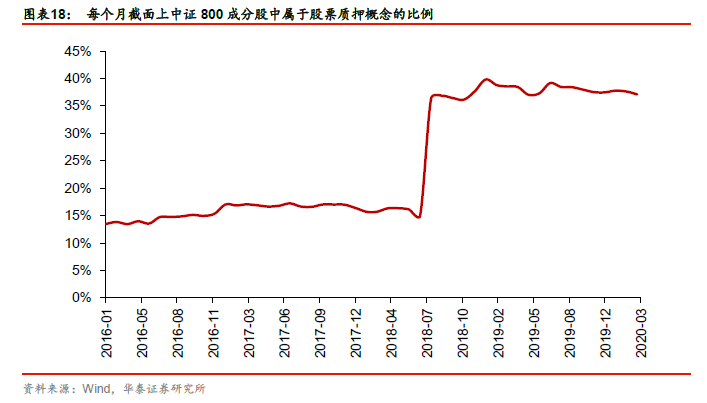
第一步：使用倾向性评分法估计因果效应

各种倾向性评分法的因果效应估计值在19中，其中倾向性评分匹配法(PSM)因果效应估计值为-0.0118，即在2016年1月至2020年3月这段时间中，属于股票质押概念的股票，其未来一个月收益的排序数相比于不属于该概念的股票要低0.0118。另外为了对比，我们计算ATE，即在不考虑任何混淆变量的情况下，属于股票质押概念的股票和不属于股票质押概念的股票的平均差异。图表20展示了三种倾向性评分法的因果效应估计值变化。

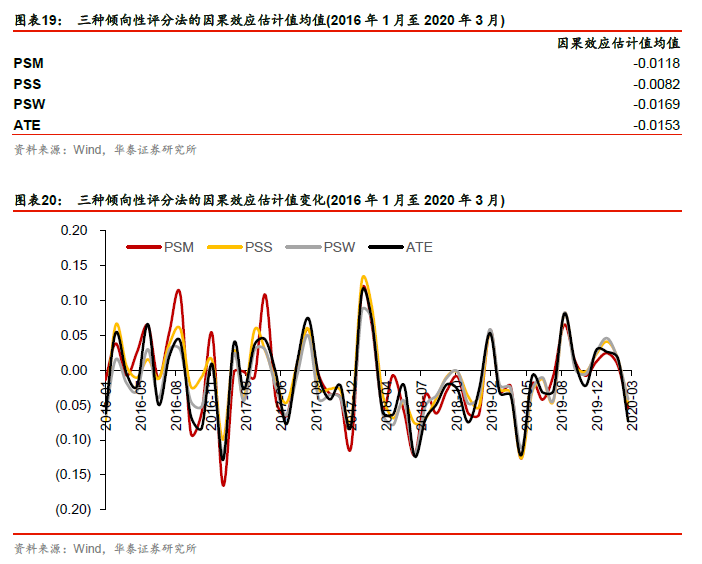
第二步：评估各倾向性评分方法的均衡性

图表21展示了各倾向性评分方法中，每个混淆变量的标准化差值stddiff。总体来看，倾向性评分加权法(PSW)中各混淆变量的标准化差值最小，说明PSW中混淆变量在处理组和对照组间较均衡，其因果效应估计值可能更可靠。

第三步：反驳

图表22展示了100次反驳测试中，三种倾向性评分法的每类反驳测试结果的均值。我们将三种倾向性评分法在真实数据下的因果效应估计值放在图表22最右侧进行对比。在安慰剂数据法中，由于生成的安慰剂数据(Placebo)替代了真实的处理变量，每个样本是否属于概念的事实已不存在，因此反驳测试中的因果估计效应下降，接近0，这反过来说明了处理变量对结果变量具有一定因果效应。在添加随机混淆变量法和子集数据法中，PSW的反驳测试结果与真实数据因果效应估计值最接近，说明其因果效应估计值可能更可靠。

预增

图表23展示了每个月截面上中证800成分股中属于预增概念的比例。

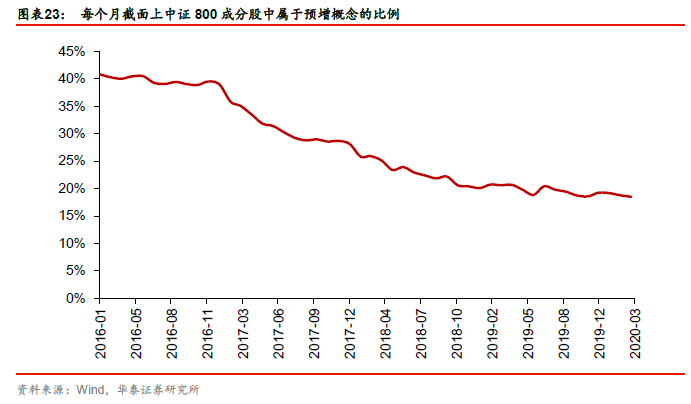
第一步：使用倾向性评分法估计因果效应

各种倾向性评分法的因果效应估计值在图表24中，其中倾向性评分匹配法(PSM)因果效应估计值为0.0138，即在2016年1月至2020年3月这段时间中，属于预增概念的股票，其未来一个月收益的排序数相比于不属于该概念的股票要高出0.0138。另外为了对比，我们计算ATE，即在不考虑任何混淆变量的情况下，属于预增概念的股票和不属于预增概念的股票的平均差异。图表25展示了三种倾向性评分法的因果效应估计值变化。可以看出，在考虑混淆变量的情形下，预增概念的因果效应估计值均值都下降了。

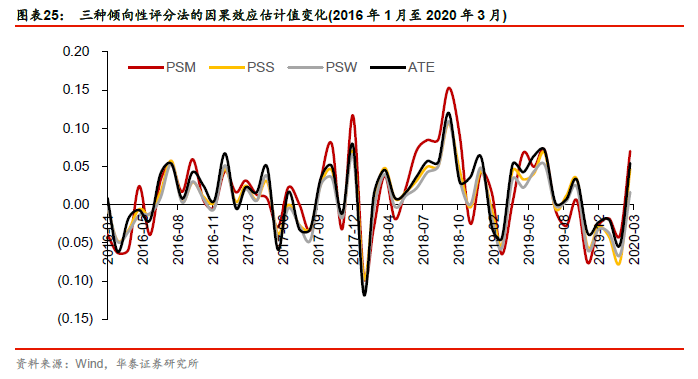
第二步：评估各倾向性评分方法的均衡性

图表26展示了各倾向性评分方法中，每个混淆变量的标准化差值stddiff。总体来看，倾向性评分加权法(PSW)中各混淆变量的标准化差值最小，说明PSW中混淆变量在处理组和对照组间较均衡，其因果效应估计值可能更可靠。

第三步：反驳

图表27展示了100次反驳测试中，三种倾向性评分法的每类反驳测试结果的均值。我们将三种倾向性评分法在真实数据下的因果效应估计值放在图表27最右侧进行对比。在添加随机混淆变量法和子集数据法中，其估计的因果效应值的绝对值已经小于安慰剂数据法，说明在对原始数据添加干预之后，因果效应已不显著，因此预增概念对于股票收益的正向因果效应是存疑的。另外，PSW的反驳测试结果与真实数据因果效应估计值最接近，说明其因果效应估计值可能更可靠。

护城河

图表28展示了每个月截面上中证800成分股中属于护城河概念的比例。

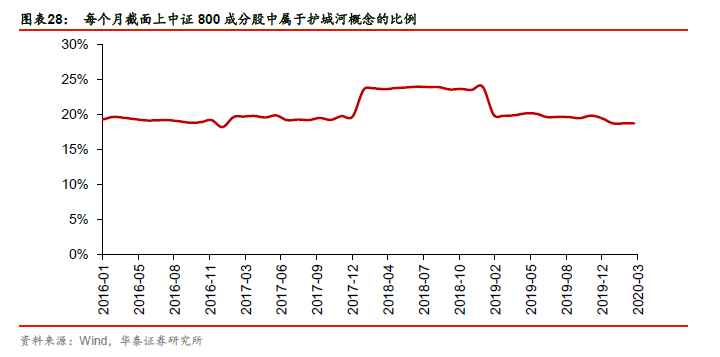
第一步：使用倾向性评分法估计因果效应

各种倾向性评分法的因果效应估计值在图表29中，其中倾向性评分匹配法(PSM)因果效应估计值为0.0205，即在2016年1月至2020年3月这段时间中，属于护城河概念的股票，其未来一个月收益的排序数相比于不属于该概念的股票要高出0.0205。另外为了对比，我们计算ATE，即在不考虑任何混淆变量的情况下，属于护城河概念的股票和不属于护城河概念的股票的平均差异。图表30展示了三种倾向性评分法的因果效应估计值变化。可以看出，在考虑混淆变量的情形下，护城河概念的因果效应估计值均值都下降了。

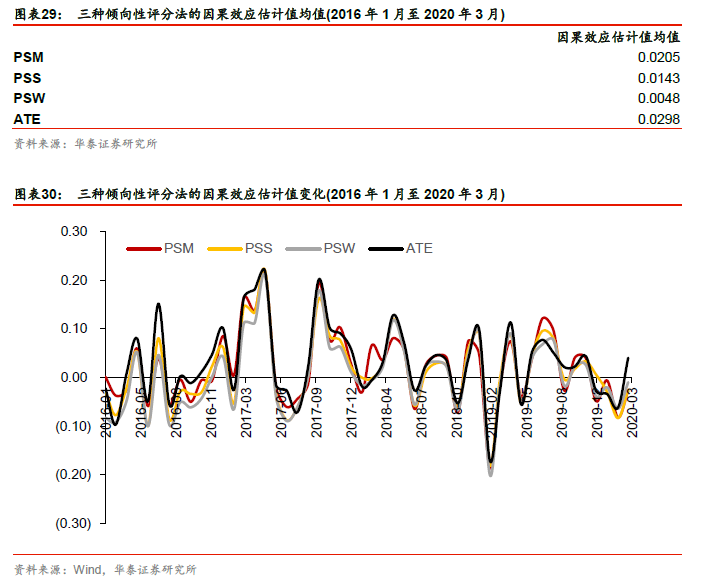
第二步：评估各倾向性评分方法的均衡性

图表31展示了各倾向性评分方法中，每个混淆变量的标准化差值stddiff。总体来看，倾向性评分加权法(PSW)中各混淆变量的标准化差值最小，说明PSW中混淆变量在处理组和对照组间较均衡，其因果效应估计值可能更可靠。

第三步：反驳

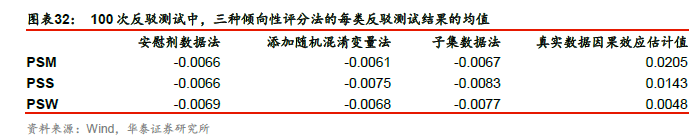
图表32展示了100次反驳测试中，三种倾向性评分法的每类反驳测试结果的均值。我们将三种倾向性评分法在真实数据下的因果效应估计值放在图表32最右侧进行对比。在添加随机混淆变量法和子集数据法中，其估计的因果效应值的绝对值与安慰剂数据法接近，说明在对原始数据添加干预之后，因果效应已不显著，因此护城河概念对于股票收益的正向因果效应是存疑的。另外，PSW的反驳测试结果与真实数据因果效应估计值最接近，说明其因果效应估计值可能更可靠。

小结

通过以上四个股票概念的因果效应估计结果可以看出，PSW在均衡性测试和反驳测试中表现都最好，可以认为其估计的因果效应较为可靠。四个概念的因果效应估计结果汇总在图表33中。通过反驳测试，我们认为基金重仓(季调)概念与股票收益有正向因果关系，股票质押概念与股票收益有反向因果关系，预增和护城河概念与股票收益的因果效应存疑。

从概念描述的角度可对因果效应的估计结果做出解释，预增和护城河概念的描述中包含较多混淆变量的信息(如净利润、利润总额)，那么在考虑混淆变量的情况下，其因果效应存疑。而对于基金重仓(季调)和股票质押概念来说，它们使用了混淆变量中所不能解释的信息，且该信息对股票收益造成了影响，因此分别具有正向和反向的因果效应。

总结

本文结论如下：

1. 机器学习本质是曲线拟合，可借助因果推断构建稳健、有推理能力的AI。现有的大部分机器学习模型是关联驱动的，关联主要有三个来源：因果关联，选择性偏差和混杂偏倚。其中选择性偏差和混杂偏倚产生的关联是不稳定的。因果推断可以帮助恢复数据中的因果关联，用于指导机器学习，实现可解释的稳定预测。对于金融市场来说，一方面市场环境持续变化的特性导致多种可观测因素的有效性都随之而变；另一方面，资产管理人对策略内部的因果逻辑和可解释性都有较高要求。这些现状都说明在将机器学习方法在运用于金融市场的策略构建时，融入因果推断的方法是一个值得尝试的方向。

2. 本文介绍了基于倾向性评分法的因果推断框架。因果推断的基本思想是在处理组和对照组间进行对照实验以估计因果效应。在观测数据中，将处理组与对照组之间分布不一样且会对结果造成影响的特征称为混淆变量，因果效应评估的关键是如何保证混淆变量在处理组与对照组的分布一致。倾向性评分法将多个混淆变量的影响用一个综合的倾向性评分来表示，降低了混淆变量的维度，使得控制混淆变量成为可能。本文归纳了倾向性评分法的三个步骤：(1)计算倾向性评分并估计因果效应；(2)评估各倾向性评分方法的均衡性；(3)通过反驳评估所估计的因果效应是否可靠。

3. 基于因果推断框架，本文研究股票所属概念和收益的因果关系。本文首先在经典的Lalonde数据集上进行因果效应估计。然后基于倾向性评分法，研究了中证800成分股中股票所属的四个概念和股票未来一个月收益的因果关系，我们选取的混淆变量为股票的基本面和量价因子暴露，考察区间为2016年1月到2020年3月。通过倾向性评分法的分析，我们认为基金重仓(季调)概念与股票收益有正向因果关系，股票质押概念与股票收益有反向因果关系，预增和护城河概念与股票收益的因果效应存疑。另外，倾向性评分加权法(PSW)在均衡性测试和反驳测试中表现都最好，可以认为其估计的因果效应较为可靠。

风险提示

风险提示：因果推断所得结论是对历史规律的总结，若未来规律发生变化，结论存在失效的风险。倾向性评分法对于因果关系的建模存在过度简化的风险。倾向性评分法中，混淆变量的选取会对因果效应估计结果造成较大影响，应谨慎对待。

参考文献

[1]Judea Pearl. Causality: Models, Reasoningand Inference. Cambridge University Press, 2009

[2]Judea Pearl, Dana Mackenzie. The Book ofWhy: The New Science of Cause and Effect. Allen Lane, 2018

[3]Peng Cui, Towards Explainable and StablePrediction.

[4]Paul R. Rosenbaum, Donald B. Rubin.Reducing Bias in Observational Studies Using Subclassification on thePropensity Score. Journal of the American Statistical Association 79(387), 1984

[5]James M. Robins, Miguel Angel Hernan, BabetteBrumback.  Marginal Structural Models andCausal Inference in Epidemiology, Epidemiology (Cambridge, Mass.) 11:550-560,2000 

[6]Austin PC. Balance diagnostics forcomparing the distribution of baseline covariates between treatment groups inpropensity-score matched samples. Statistics in medicine,2009.

免责声明与评级说明

公众平台免责申明

免责声明：自媒体综合提供的内容均源自自媒体，版权归原作者所有，转载请联系原作者并获许可。文章观点仅代表作者本人，不代表新浪立场。若内容涉及投资建议，仅供参考勿作为投资依据。投资有风险，入市需谨慎。