来源:投资家
讲一个大家可能耳熟能详的故事吧。
在华盛顿州西雅图附近出现了有史以来最伟大的一位电脑编程员。他意识到生产电脑芯片的英特尔是个朝阳企业,并且最早预测微型计算机必将大有市场。所以他决定为还未见起色的计算机编写软件。
20世纪70年代中叶,他自创公司,专门销售微型计算机所需的软件。公司成立伊始,“一切都显得很荒唐离谱”,“公司的员工穿个裤衩,光着脚就来上班了”,“西装革履的无一例外都是来访者”。
但这个名不见经传的小公司很快就财源滚滚。到了1981年,公司的操作系统在配备有英特尔微型处理器的个人电脑领域占据了绝对的市场份额。
公司初期取得了一系列成果,但接着却面临了一个分水岭时刻。IBM于1980年夏前来拜访,讨论新一代个人电脑的操作系统合作。经过几轮磋商,两个公司达成一致协议。
1981年8月,电脑零售商在销售新一代IBM个人电脑时附带销售这个新公司的软件。公司的命运就此改变。之后的故事想必很多人都已知晓。
也许一些人对故事的后半部分不太熟悉,我还是再多说几句吧。1994年7月8日,这位计算机技术的开拓者走进了位于加州蒙特利的一家飙车族酒吧。
他身穿摩托车皮夹克,可能他与人发生了争斗,也可能无意中从高处跌落,总之这位开拓者头部受到重创,扎挣着离开了酒吧,三天后死于伤势加重和慢性酒精中毒,年仅52岁。他被安葬在西雅图,墓碑上刻着软盘的图案。
他就是加里·基尔代尔。
你也许以为故事的主人公是微软创始人-比尔·盖茨。从故事的前半部分看,这样想也不无道理。如果基尔代尔没有英年早逝,他有没有可能成为世界首富呢?
只是历史是不能假设的。后来,IBM没能与基尔代尔做成生意,盖茨就自告奋勇揽下了这笔生意……
当人们问起微软的成功在多大程度上靠的是运气时,盖茨说“运气占相当大一部分”,“我们把握住好时机不完全靠运气,但是没有好运就没有微软的今天。”
我们的生活中,处处充满运气,我们对一个成功结果的评定,很难将实力和运气区分开来。
这也是金融从业者迈克尔·莫布森所关心的方向,出生于1964年的莫布森毕业于乔治城大学,现任职于摩根史坦利投资管理公司,之前曾在瑞士信贷、蓝山资本等工作过。除此以外,他还长期担任哥伦比亚商学院的客座教授,以及复杂科学研究的发源地——圣塔菲研究所的董事会成员。
他于2012年出版《实力、运气与成功》一书(The Success Equation),聚焦于实力与运气在商业、体育及投资领域中的作用,并运用多学科思维模型对其深入分析探讨。
对辨别一项活动需不需要实力,他提供了一个快速的方法:问一下自己失败是不是因为自己不想赢。在靠实力取胜的活动中,自己不想赢就可以不赢;但玩轮盘赌或买彩票,再也不想赢也可能会赢。
而我们生活中常常试图对于不能左右的“运气”加以控制,而在自己能提高的“实力”上却不加以努力。
美国神学家尼布尔的写于1934年的经典安宁祷文曾说:
神啊,请赐予我内心安宁以接受我所不能改变的,请赐予我勇气以改变我所能改变的,请赐予我智慧以分辨这二者之间的差别。
莫布森正是希望给读者以智慧去分辨实力和运气,以下选择《实力、运气与成功》第六章《运气的表现形式:流行为什么成为流行?》,祝开卷有益!
在一些领域,运气的钟形分布曲线或者独立事件就可以解释很多现象。然而在娱乐世界里,成功和失败都是社会相互作用的结果,根本无法预测结局。
对于一个事件,人们往往会评定很多等级,个人的观念也很容易被他人的评价左右,一系列不确定因素让成功来得太突然,失败来得太令人费解。电影编剧威廉·高德曼不禁说了这样一句俏皮话:“世人一无所知。”
举个例子吧。假设一首歌比另一首歌在某段时间稍微流行些,在人们的相互影响下前一首歌就会越来越流行。本来两首歌是同等水平、同样的欣赏价值,最后却一个唱遍大江南北,一个渐渐无人问津,这种现象就是“累积效应”。
“累积效应”让人们几乎没法预测成功。实力当然对结果的好坏有影响,但是运气的影响却是压倒性的。我们可以仔细探究下这种现象、背后的原理以及令人感到意外的结果。
社会的影响以及累积效应往往使得一个事件呈幂次定律分布。图6-5显示的是2010年美国最大的275个城市的排名和人口情况。横轴是城市的排名,纵轴是城市的人口。图中的城市分布大致在同一条斜线上,正好可以用幂次定律来表达。
通过幂次定律可以得出美国第17大城市得克萨斯州圣安东尼奥市的人口为132.5万,美国第70大城市纽约的布法罗人口为26万。
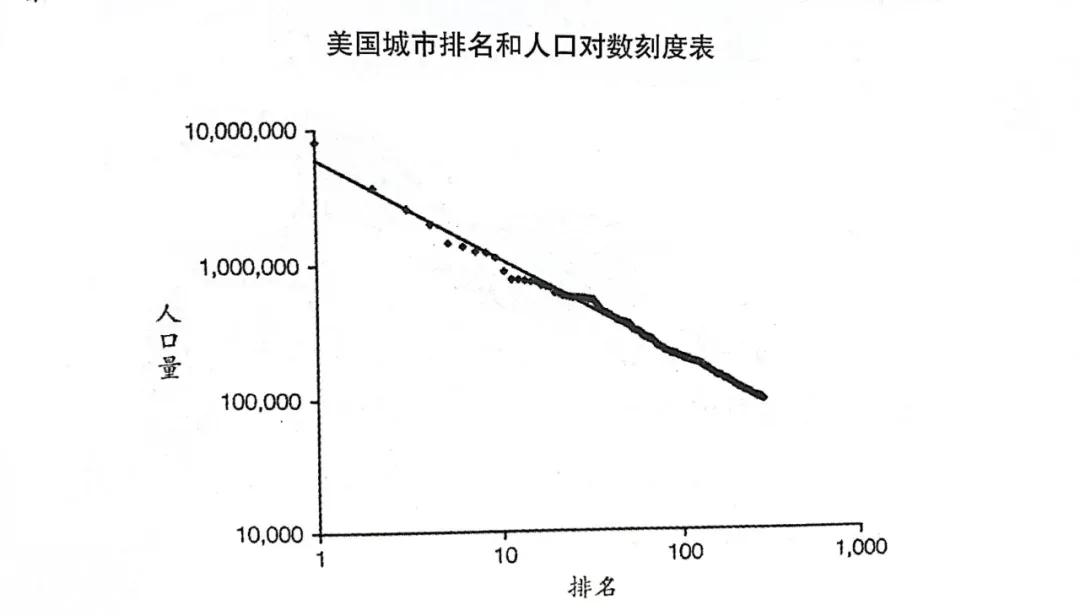 图6-5
图6-5幂次定律来自这样一个事实,指数(或幂)决定斜率。很多社会现象都遵循幂次定律,比如说图书销售的排名和销量、科技论文的排名和引用率、恐怖活动地区的排名和死亡人数,以及战争的规模和遇难人数等。
遵循幂次定律分布的事件具有的主要特征是大值很少,小值很多,所以算均值没有任何意义。就比如图书销售,市场上的上百万本图书,前十名的每年能卖出100多万本,而有的图书每年卖的还不足100本。
畅销书总是屈指可数,却无疑是最大的赢家;无人问津的书数不胜数,却是商业竞争的牺牲品。由于畅销书的数量有限(即样本很少),很难说哪些畅销书作家是靠文笔、思想或是内容(即实力)取胜。而且实力本身也不足以解释幂次定律现象,所以我们有必要寻找这种两极分化现象背后的原理。
区分独立结果和相依结果很关键。棒球运动员本场的比赛不受上一场成绩的影响是不可能的。但是在一个赛季,这种影响就微乎其微,每场比赛可以看成独立事件。
现在我们引入一个新的概念-路径依赖过程,就是前面发生的事决定后面发生的事,也就是过程环环相扣。
 图:迈克尔·莫布森
图:迈克尔·莫布森这一过程的初始条件对后面的影响至关重大,比如说富人会越来越富,穷人会越来越穷。哥伦比亚大学知名的社会学家罗伯特·默顿将这一现象称为“马太效应”。在《圣经·新约·马太福音》中有一句名言:“凡有的,还要加给他叫他多余;没有的,连他所有的也要夺过来。”
假设两名能力相当的研究生去应聘大学教授职位,一位有幸被常春藤大学录用,另一位则被一所名气差些的学校录取。前者辅导的学生更优秀,教学任务更轻些,工作同事的学术水平更高,研究所得的酬劳也更丰厚。
在这种氛围中他发表的学术论文就多,论文被引用的次数也多,名气也就越来越大。这样在退休时,两人的名声、地位就有了天壤之别。虽然马太效应讲的是同一起跑线上的两人最后却天差地别,但是道理却是一样的。
初始条件很关键,随着时间的推移,微弱的优势渐渐明显起来。
这一现象背后有很多原理,其一就是“优先链接”。比如说你开发了一个新的网站,希望越来越多的人看到这个网站。最高效可行的办法就是将新网站的网址链接到知名网站如谷歌、维基百科上,而不是链接到那些少人问津的网站。
知名网站的访问量大,会带来正反馈:知道新网站的人越多,访问量就越来越大。通过优先链接,一些新网站的访问量会逐渐增大,而另外的网站会因访问量太少而被淘汰。初始的一点点优势,就像星星之火,渐渐就形成了绝对优势。
我们做个很简单的模型试验说明这一过程。假设你有一个罐子,里面装了5个红色弹珠、4个黑色弹珠、3个黄色弹珠、2个绿色弹珠、1个蓝色弹珠。
现在你闭上眼睛,随机摸一个弹珠。假如你摸到的是黑色的,将黑色弹珠放回罐子时再多放一个黑色的,那么罐子中就有5个黑色弹珠,其他颜色的弹珠数目不变。然后重复这一过程,随机摸一个,放回后,再多放一个同样颜色的弹珠。重复100次后,罐子满了。
起初,罐子中一种颜色的弹珠越多,随机被摸中的概率越大,比如15个弹珠中3个是黄色的,摸中黄色的概率就为20%(3/15)。
大家很容易看出这是个路径依赖过程。如果第一次摸的是黄色弹珠,下次摸到黄球的概率就上升为25%(4/16)。不过尽管第一次摸中的弹珠颜色让它有了累积的优势,预测最后的赢家却还是很难。
图6-6显示的是电脑三次模拟这一过程的曲线图。第一幅图红色弹珠被摸到的次数最多;第二幅图黄色弹珠最多,其次是红色弹珠;第三幅图的结果令人很意外,蓝色弹珠最多。
你可以把不同颜色的弹珠想象成实力,数目越多代表实力越强。实力最强的弹珠得胜的概率最大,但并不能保证一定会取胜。
 图6-6
图6-6运气将初始实力分布不断洗牌,使得最后的结果千差万别,难以预测。
而且一旦某种颜色一直遥遥领先,游戏就可以说结束了,因为优先链接已经将结果定形。虽然模型比现实生活中的事件简单多了,但它仍然反映了在路径依赖过程中成功和实力并没有必然的关系。
在马太效应中临界点和转折期也至关重要。转折期中,小的累积性变导致了规模效应,这一关键点也俗称转折点。冰箱中放杯水,水会在临界点0℃变成冰。在临界点温度的些许变化就会产生液体到固体的变化。社会体系中同样存在这样的临界点和转折期。
斯坦福大学社会学教授马克·格兰诺维特建立了一个简单模型来演示临界点的重要性。假设有一百个潜在的聚众闹事者在公共广场上闲逛,每人都有一定的“暴动阈值”-就是闹事者最低有多少人时他们才加入。
比如说第一个人的“暴动阈值”为零(即煽动者),后面的人为1,再后面的为2,顺次延到99。这种“暴动阈值”的递增营造了“多米诺骨牌效应”,导致暴动的发生。这就好比“破窗效应”,好事者用石头砸了窗玻璃,很多人顺次加入,最后就变成了聚众砸破窗的闹事。
现在我们稍微改变下初始条件:将“暴动阈值”为1的人直接换成“暴动阈值”为2的人。可以推断,这种情况下暴动事件就不会发生了。媒体上将第一群人称为“刁民”,第二群人称为“良民”。而实际上,这两类人在本质上是一样的。仅仅是“暴动阈值”上的微小变动,就可能化暴动为和平。
上面的例子虽然很简单,却能让我们明白更为现实的问题,如创新技术的应用(iPad的流行)、美国迈阿密减肥法的推行、时尚潮流的兴起(如瑜伽衣),甚至疾病的传播(如流感)。一旦小的创新有了一定的认知度,它的成功就成定局了。同理,如果形不成多米诺骨牌效应,伟大的创新也可能夭折。
在经济学中,这种两极分化现象常常有两个原因:日益增长的收益和网络效应。传统的经济学理论以收益递减为根本。当一件商品供不应求时,价格会上升,生产者的收益会增加。
高额的收益吸引了大批竞争对手,他们也投入生产,最终平衡供需关系,从而使商品价格回落。这个过程就是负反馈,平衡两极差距,使强的变弱,弱的变强。
在不同的经济领域,负反馈不能都给人以满意的解释,因为正反馈往往居于上风。最经典的例子是对特定的技术确定统一的规格标准。20世纪70年代,家用录像系统(VHS)和首款独立盒式录像机(Betamax)互相竞争市场份额。
近年来,索尼与松下电气开发蓝光光盘(Blue-ray)与东芝发展高分辨率光盘(HD DVD)也明争暗斗,抢占市场。这种技术角逐是个“赢家通吃”的过程,谁占上风谁就垄断了市场。
20世纪70年代中叶,VHS和Betamax势均力敌,平分市场。但是VHS略占上风后,便在短短几年内窃走了90%的市场份额。总的说来,富者越富,穷者越穷。
收益递增总是伴随着高昂的前期成本、低增值成本以及网络效应(即人气或口碑)。
微软在个人电脑操作系统上的优势充分体现了收益递增的整个过程。微软的第一代视窗系统(Windows)花费了大量的精力和时间,前期的成本非常高,但是制作附加的副本--软盘的成本就非常低(当时,软件都要配置软盘的)。因为业界标准使得人们可以进行文件交换,网络效应对操作系统和相关的电脑程序的影响就变得很大。随着业界标准在群众中受到广泛的认可,越来越多的电脑程序员开始为Windows开发软件,这更加促进了Windows的流行。被广泛运用的产品能给人们带来更大的价值,因此人们对它的需求量就比较大,生产者最后的利润也就越多。这就是需求的规模经济。
将软件经济学和网络效应结合起来,就会达到收益增值。胜利者的利润飙升,财运势不可挡,而初期不相上下的竞争对手却很难分一杯羹。探讨幂次效应背后的原理就是要看初始条件,关键的转折期怎样形成,看市场的两极分化。
实力并不是在竞争中获胜的保障,运气才是。可以说,这些所谓的市场机制就是运气的层层叠加。

VIP课程推荐
APP专享直播
热门推荐
收起
24小时滚动播报最新的财经资讯和视频,更多粉丝福利扫描二维码关注(sinafinance)








