不支持Flash
|
|
|
研究报告：期货品种投资绩效评价体系的构建http://www.sina.com.cn 2007年06月15日 00:11 国泰君安
本研究的目的是通过对期货合约历史交易价格的分析来度量期货投资的风险收益，并以此来判断评价不同期货品种的投资价值。在现代金融理论中，对任何一种金融产品的评价都要考虑到风险和收益这两个紧密联系的方面。自从马克维茨1952年发表《资产选择》一文以来，西方许多金融经济学家一直以来都在致力于金融产品收益和风险度量的研究，并行成了许多成熟的度量评价方法(特别是对风险的度量)。我们在考察和分析了已有的度量方法和评价体系的基础上，结合我们研究问题的实际提出了我们自己的度量和评价体系。 一.风险收益的衡量与分析 1.收益的衡量 一直以来，人们对于收益的衡量方法比较一致，这也从另外一个方面反应了人们对于风险的关注。马克维茨1952年在《资产选择》一文中，用预期收益作为资产未来收益水平的代表。此处，马克维茨研究的是资产配置问题，是一种事前的风险收益度量问题。因此，预期收益的计算要以未来资产价值的概率分布为前提。而我们此处是一种事后的评估，是从已经发生的价格序列来估计收益，二者之间是不同的(当然，有时候以历史数据计算出的收益率作为未来预期收益率的估计值，这只是一种合理的近似)。一般地讲，金融资产的收益包含两部分，期间的现金流入和资本溢价(即持有期间资产价格的变动情况)。因此简单收益率回报可以表示为 2.风险的衡量 相对于收益的度量讲，风险的度量就没有那么简单明晰了。半个世纪以来，面对风险的巨大压力，人们对风险度量的理论和方法进行了不懈的探索，直到上个世纪50年代后，风险度量才逐步完成其基础性的研究成果，包括： (1)马科维茨的方差 方法 马柯维兹在1952年发表的《资产组合的选择》一文阐述了均值—方差理论，该理论将统计学中期望与方差的概念引入资产组合问题的研究，在假定收益率的概率分布确定的情况下，来度量收益率这一随机变量相对平均收益率水平的总体平均离差。提出用资产收益率的期望来度量预期收益，用资产收益的标准差来度量风险的思想，将风险定量化。所谓方差就是指收益率偏离均值的程度。其计算公式为： (2)罗伊的“安全第一”法则与马柯维兹的半方差方法。罗伊在1958年发表了投资组织理论的有影响的论文。他相信，一个投资者很难找到一个数学公式来量化效用函数，因此，他致力于找到一种可行的方法来确定风险—收益权衡的最佳比例。按照罗伊的理论，投资者会更倾向于“安全第一”法则，因此会设置最低可接受收益率。罗伊称这个最低可接受收益率水平为“灾难性水平(Disaster Level)”。投资者会倾向于使投资收益低于“灾难性水平”的可能性最小。因此，通过最大化收益与方差的比率，投资者可以选择使得投资收益低于“灾难性水平”的概率最小的投资组合。收益—方差比率使得投资者可以将投资组合的损失高于“灾难性水平”的可能性极小化。 马柯维兹在1959年意识到罗伊的思想的重要性，便阐述了均值—方差分析的局限性。作为一种风险度量方法，方差法可能会与投资者的偏好结构以及证券和投资组合的回报率分布状况发生脱节，使得均值—方差所带来的信息无法充分区分不同的收益分布状况。投资者出于以下两个原因会对下半方差更感兴趣：第一，只有下半方差才与投资者相关；第二，投资组合收益的分布可能不是正态分布。于是马柯维兹提出了两个思路来衡量下半方差：利用平均收益为基准来度量下半方差，以及利用目标收益为基准来衡量下半方差。这两种方法仅仅计算低于平均收益或低于目标收益的收益串的方差。由于只有收益分布的一半被使用来计算方差，因此，马柯维兹称这种计算风险的方法为部分方差或半方差法。 (2) LPM类尾部风险(downside risk)衡量 1994年Leslie A.Balzer 提出了损失概率( Probability of Shortfall )指标来衡量风险大小。损失概率指出了资产收益低于某一参考点的概率。参考点一般情况下设为零，但是也可以设定为其他任何可以接受的最低水平。特别的，当参考点设为市场组合收益率时，我们可以考察资产相对于市场大势的表现情况，是比大势表现好还是差。指标的计算公式为： Probability of Shortfall= Probability(R 其中，R是指投资的收益率，B是所选择的基准收益率。 损失概率指标虽然给出了资产收益低于参考点的可能性，但是并没有给出损失的严重程度的信息。比如，同样是20%的概率资产收益低于0，但是一个损失价值的20%，一个损失价值的100%，显然这两种资产的风险也是不同的。考虑到这一情况，我们提出了另一个修正指标——预期损失(Expected shortfall)。这个指标不仅考虑到了收益低于基准的可能性，而且包含了每一可能性发生情况下的损失情况，比较全面。其计算公式为： Expected shortfall＝E[R-B], where R-B<0 该指标的一个最大的问题是没有考虑到，人们对于小概率大损失和大概率小损失的不同感受和厌恶程度。一般情况下，人们更厌恶那些小概率大损失的情况，这也是人们平时最经常感受到的风险的概念。而在该指标中，大损失和小损失只是和它们相应发生的概率相乘并加总，也就是说这两种情况被赋予了相同的权重，这显然是不符合现实的。这个不足在Harlow提出的LPM类指标(具体的是指下半方差指标)中的到了解决。 1991年Harlow提出了LPMs(lower partial moments)指标来度量风险。该指标也是度量低于基准收益的风险，其中partial是指该指标只衡量了收益分布相对于基准收益一侧的情况，lower是指该指标衡量的是资产收益低于基准收益的损失风险(downside risk)。LPM风险度量理论将投资者从传统的单一效用函数(指方差和半方差的二次函数)的束缚中解脱了出来。引入了多重符合凡·纽曼—摩根斯坦原则的效用函数。LPM理论几乎涵盖了所有人的风险厌恶程度：从风险偏好到风险中性，再到风险厌恶。其表达式为： 其中n是LPM类指标的阶，代表了投资者的风险厌恶程度。N取不同的值，我们可以得到前面的度量指标。比如，当n=0时，LPM指标上文的损失概率( Probability of Shortfall )指标是一致的；当n=1时, LPM指标等于上文中的预期损失(Expected shortfall)指标。当n=2时，LPM指标变为下半偏方差，该指标很好的克服了人们对于小概率大损失和大概率小损失的不同感受和厌恶程度这一现实问题，因为这两种情况被赋予了大小不同的权重。特别的，当n=2，并且基准收益时预期平均收益时，LPM指标就成了马克维茨提出的下半方差(semivariance)指标。下半方差指标衡量风险具有很多优点，澄清和考虑了许多有关风险的内涵。包括，考虑到了人们对风险和收益感受的不对称性，以及对小概率大损失和大概率小损失事件的不同感受和厌恶程度等，可以说是最符合人们行为的风险度量指标。但是，下半方差指标也有不足之处。首先，该指标不像方差指标简单明了，人们对他的了解和理解不够，在实际应用中比较少。其次，基准指标的选择缺乏统一的标准，选择不同的基准指标会产生不同的风险度量结果。最后，在分析由众多资产组成的资产组合时，用下半方差指标比用方差指标更为困难。因为，用下半方差指标时，整个组合的风险不像使用方差指标时那样容易的分解为单个资产风险的函数，这样在计算组合的风险时必须把它当作一个整体来处理，而不能够像方差指标那样通过单个资产的风险集成得到。 针对方差指标的问题，学者们提出了一类尾部风险的度量方法，这一类方法很好的解决了方差指标所面临的困难。这类指标主要衡量相对于人们事前确定的基准而言，资产收益低于基准收益的风险。由于定义的不同，它很好的克服了方差指标的所面临的两个主要问题。首先，它不需要以收益分布的对称为条件，因为它考虑的是收益的尾部分布风险(即小于基准收益部分的风险)。再者，它考虑到了人们对于受益和损失的不同感受，只考虑了相对于基准而言的损失的风险。 (3)VaR方法 VaR(Value-at-Risk)，即在险价值，按照Philippe Jorion的定义是指：在正常的市场环境下，给定一定的时间区间和置信水平，测度预期最大损失的方法。 定义c为置信水平,X为资产组合的损益，则一定持有期(T)内的VaR(为正值，表示损失的绝对额)定义为： VaR值即为一定置信水平下，资产组合在未来T期内的最大损失，也就是损益X概率分布的分位数。 根据定义，VaR同时给出了市场风险暴露的大小和发生损失的概率。VaR的计算可以采用正态分析法、历史模拟法、蒙特卡罗模拟法等方法。历史模拟法是基于投资组合的历史表现估计未来的可能损失，从而得出投资组合的在险价值。而蒙特卡罗法则是通过能描述市场因素可能变化的统计分布，从而估计未来可能的损益分布，得出在险价值。 90年代以来，随着风险管理和控制理论的发展，VaR作为风险的度量被越来越广泛的采用。VaR作为风险管理和控制的新工具，很好的表达了投资者所关注的损失。但是VaR仅仅给出了一定置信水平下的最大可能损失，而实际的损失可能远远大于VaR值，对于收益分布为后尾的情况而言更是如此。例如，某一资产组合99%置信水平下的VaR值为100万，根据VaR值我们可以推断未来一段时间内可以在99%的水平下保证最大损失不超过100万，但实际情况可能是尾部1%的损益发生了，比如说实际上损失了500万。可以看出VaR方法的缺陷就是忽略了尾部分布的信息，可能导致实际的损失远大于VaR值。我们不但想知道发生c个百分点的界限损失，而且也想知道在其超过临界值时发生损失的平均规模。为此，人们提出了条件VaR(C-VaR)的概念作为VaR的有益补充。所谓条件VaR就是指损失超过VaR值的平均值，定义资产组合损益X的分布函数为f(x),则有： 这个数量又被称为预期不足额(expected shortfall)、条件损失(conditional loss)、尾部损失(tail loss)等，很好的回答了这样一个问题：如果遇到风险价值以外的风险，我们将损失多少？ 对于标准正态分布而言，我们可以很容易的计算出一定置信水平的分位数(VaR)和条件VaR值(Cvar)，见下表： 置信水平（ %） 99.99 99.9 99 97.72 97.5 95 90 84.13 50 分位数 -3.715 -3.090 -2.326 -2.000 -1.960 -1.645 -1.282 -1.000 -0.000 cvar -4.018 -3.370 -2.667 -2.368 -2.338 -2.062 -1.754 -1.525 -0.798 可以看出，在标准正态分布下VaR与 条件VaR(C-VaR )并不是相差太多，特别是当置信水平比较高时，比如在99%的置信水平下VaR为2.326， C-VaR为2.667。实际上当置信水平增加时，C-VaR与VaR的比率收敛于1，因此在正态分布情况下用VaR值来衡量潜在的损失是恰当的，能够比较全面地反映风险的大小。但是当分布不是正态分布时，特别是对于存在厚尾分布的资产收益率而言，一定置信水平下的VaR与C-VaR可能相差很远，此时的VaR并不能全面反映潜在的风险水平。这一点我们从下面的分析中就可以看得出。 Merriken(1994)指出，作为风险度量的方法，方差指标和LPM类指标适合于进行短期投资分析。这与我们进行的研究是相吻合的，因为在期货市场上大部分投资者进行的都是短期投资。基于上面的分析，我们此处准备用方差，LPM类指标(其中n=2，基准分别取无风险利率，市场利率和预期收益率)以及VaR指标(包括条件VaR)来分别度量风险，并进行比较分析。 3.风险调整的收益率 单独用收益率或者是风险指标来评价金融资产的绩效都是不全面的，必须把风险和收益结合起来考虑，即考察风险调整的收益率指标。用收益除以风险就得到了风险调整的收益率，该指标反应了承担单位风险所获得的收益状况，该指标越大表明资产的绩效越好，投资价值越大。收益率指标我们采用对数收益率，风险指标我们分别采用方差，LPM类指标(其中n=2，我们假定投资者为风险厌恶者，基准分别取无风险利率，市场利率和预期收益率)以及VaR指标，由此我们构造出了三大类风险调整的收益率指标来评估期货合约的投资价值。 (1)Sharp比率指标：Si＝(Ri-Rf)／σi (2)LPM比率指标 LPMi=(Ri-Rf)/ LPM，其中n=2，基准分别取无风险利率，市场利率和预期收益率. (3)RAROC模型 以VaR作为风险度量的RAROC模型的其计算公式为： RAROC＝ROC／VaR(C-VaR) 其中，ROC为评价期内资产的收益率，VaR为证券组合在该评价期和给定的置信区间内预期的最大损失值。 这三类比率主要的区别在于风险度量指标的不同，它们的忧缺点上文中已经分析过，在此不在重复。还有，我们在此使用的风险度量指标都是总体风险指标，并没有对风险进行诸如CAPM模型之类的系统性风险和特有风险的分解。我们没有考虑分散化的影响，对于我们所分析的期货投资而言是合适的，同时也是一种稳健的分析方法。 二.流动性的考察 流动性是金融市场赖以存在与运行的基石,因而,期货市场的流动性对于市场中期货品种能否迅速及时达成交易并发挥其应有功能是非常重要的。合理的流动性为期货市场中各种类型的投资者提供了快速、低成本买卖期货合约的机会,而在一个缺少流动性的期货市场中买卖双方很难在满意的价位完成预期数量的交易,期货合约的交易将逐渐萎缩并最终被淘汰出局。期货合约交易流动性的急剧下降将使得期货市场不能充分汇聚各方面信息,并通过公开竞价的交易机制形成公正透明的价格,所以,其发现价格以指导相关企业生产和经营的作用,以及为套期保值者规避现货市场价格风险以锁定成本和利润的功能将受到不利的影响。因此，我们再分析各个期货品种的风险收益，确定其市场价格表现的基础上要进一步的分析不同品种的流动性状况，这也是投资者在选择投资品种时的一个重要的考虑因素。 对市场流动性的研究是和市场微观结构理论的研究紧密联系在一起的,不同的市场微观结构基础形成了市场间不同的运行特征。因此,同样是对市场流动性的衡量,不同的市场使用的考察指标之间存在一定差异,例如,作为市场微观结构的基础,市场的交易机制依据其价格发现机制的不同可分为两类:一类是报价驱动型,一类是指令驱动型。国外的证券市场和期货市场较多采用做市商制度,也就是报价驱动型市场,因此,国外对市场流动性研究的指标设计基本上是基于报价驱动型市场,例如,纽约证券交易所通常是使用价差指标和价格改善指标来衡量市场的流动性。但是我国国内的证券市场和期货市场采用的都是指令驱动型的计算机自动撮合的交易系统,没有做市商制度,因此,适合国外证券市场的流动性指标并不能直接拿来度量国内市场的流动性。在报价驱动型市场中,做市商为市场的交易提供流动性,交易者可以以给定的做市商的报价迅速执行交易,市场流动性的特点在于交易的即时性。在指令驱动型市场中,交易双方是根据掌握的历史信息(现在及过去的) 对未来的价格和交易量进行预期,反映不同投资者预期的指令通过经纪人交到交易所后按照一定的成交原则成交。不同的预期产生不同的未来时刻的价格和交易量,如果到达市场的买卖指令出现不匹配,那么就会有部分投资者的指令得不到执行,市场的流动性就会下降。由此可见,在指令驱动型市场中,市场流动性的特点是和市场较大交易量的影响及指令出现不匹配时可能面临的隐性交易成本有紧密联系的。 衡量市场流动性的方法可以分为四种类型,即价格法、交易量法、价量结合法和时间法。其中时间法衡量交易的即时性,主要是使用日内高频数据分析订单到达市场到执行之间的间隔或是一个特定时间内的交易次数,由于收集日内高频交易数据的困难,所以,在本文不讨论时间法的使用。价格和交易量同时都是反映市场流动性的重要指标,所以,价格和交易量必然与市场的流动性之间存在着深刻的内在联系。 Barclay和Smith (1988) 给出了价格及交易量与流动性之间的内在关系:价格与流动性呈负相关关系,绝对价差随价格上涨而增加,市场深度随价格上涨而降低;交易量与流动性呈正相关关系,价差随交易量的增加而减小,市场深度随交易量的增加而增大。价格法是通过衡量市场宽度来考察流动性的,这种方法的衡量指标主要有价差衡量指标、价格改善指标、价格自相关模型等。在采用报价驱动型的市场中,价格法能够较好地反映出市场的流动性状况。交易量法是基于市场交易量的流动性衡量方法,衡量指标主要有市场深度、成交深度、深度改进率、换手率等。交易量法忽略了价格变化这一衡量市场流动性最重要的因素。因为交易量大小与价格波动性有关,而市场价格的波动性又会对市场的流动性产生影响,所以,忽略价格变化的交易量法在衡量市场的流动性存在着较大的局限性。价量结合法结合了价格和交易量的方法,较好地克服了单纯的价格法和单纯的交易量法的不足,比较适合用来分析采用指令驱动型市场交易机制的市场流动性,例如我国证券和期货市场的流动性。 Kyle 等(1985) 将价格和交易量结合起来衡量市场的流动性,提出了一个市场深度模型,用于分析净交易行为对价格的影响程度。模型如下: P( y) = μ+λy , D =1/λ 其中P(y) 是证券价格,y 是该证券的交易量,μ是证券的真实价值,λ代表证券价格对交易量的敏感程度,D 是衡量市场深度的指标。D 越大的证券,其价格就越不容易受交易的冲击,从而其流动性也就更好。以这一模型为基础,衍生出一系列以成交量与价格变动之间关系来衡量市场流动性的流动比率指标,如Amivest 流动性比率、Martin 流动性比率、Hui-Heubel 流动性比率等。其中, Hui- Heubel 流动性比率将证券的流通市值纳入到指标当中,使其对单个证券或是整个市场的流动性衡量更为合理。 结合期货合约的特点,本文使用如下指标来检验我国期货市场的流动性: 其中,Ft 是期货当前收盘价格, 三 研究方法设计 本文研究的期货品种为国内三家期货交易所10个期货品种, 即上海期货交易所的铜、铝、橡胶、燃料油, 大连商品期货交易所的大豆、玉米、豆粕, 郑州商品交易所的硬麦、强筋麦、棉花。研究所用数据为每个期货合约的日交易数据, 包括开盘价、最高价、最低价、收盘价、交易量和持仓量。数据的时间跨度范围为：铜、大豆从1996-2-7～ 2004-12-31, 铝从1996-2-9～ 2004-12-31, 橡胶、小麦从1997-2-9～ 2004-12-31。 同时考虑到我国期货合约交易的特点，即刚上市时交易量比较少，在合约到期交割之前的3-4个月交易比较活跃，流动性比较好，随着交割日期的临近交易量又开始减少。因此，投资者一般都只买卖市场上所谓的主力和约进行投资，很少投资于其他合约，对于广大投机者而言更是如此。也就是说，每一个期货合约对于投资者而言实际上只有一段时间在进行集中的交易，所以我们考虑构造连续和约来分析投资者的风险收益情况，这对于分析每个交易品种的流动性也是合理的。具体的，连续和约的构造方法为：对于铜、大豆, 由于交易量较大、交易较活跃的期货合约往往是距离当前月之后(不包括当前月) 的第4个期货合约, 故对铜和大豆, 连续期货合约选取距离当前月之后的第4个期货合约作为代表, 在最近期期货合约进入交割月之后, 然后再选取下个距离当前月之后的第4个期货合约, 这样就得到一个连续的期货合约序列。而对于铝、小麦和橡胶, 交易量较大、交易较活跃的期货合约往往是距离当前月之后(不包括当前月) 的第2个期货合约, 因此, 对铝、小麦和橡胶, 连续期货合约选取距离当前月之后的第2个期货合约作为代表, 在最近期期货合约进入交割月后, 选取下个距离当前月之后的第2个期货合约。同样以铜和大豆为例, 说明连续合约的产生过程, 假设现在的时间是1997201, 对铜来说, 距离当前月的第4个合约是1997205 交割的期货合约,而到1997202, 距离当前月的第4个合约是1997206交割的期货合约, 因此, 在1997201 选取1997205 交割的期货合约作为代表, 而到1997202 选取1997206交割的期货合约作为代表, 以此类推; 对于大豆, 假设现在的时间是1997201 或02, 距离当前月的第4个合约是1997209 交割的期货合约, 而到1997203或04, 则距离当前月的第4个合约是1997211 交割的期货合约, 因此, 在1997201 和02 选取1997209交割的期货合约作为代表, 而到1997203 和04 选取1997211 份交割的期货合约作为代表, 以此类推。这样产生的连续期货合约优点在于期货交易相对较活跃, 期货价格、交易量、持仓量具有较好的代表性。在连续合约中, 铜、大豆的时间跨度从1997-01-02～2004-12-31, 铝的时间跨度为1997-1-8～2004-12-31，小麦、橡胶的时间跨度从1998-1-5～2004-12-31。 首先，我们分别计算每个期货品种的收益率，风险，风险调整的收益率等指标，根据每个指标给出具体的绩效排名次序。特别的，在考虑LPM类风险指标实时，对于基准的选择，我们考察无风险利率，市场指数收益率和与平均收益率三个基准。其中，无风险利率我们选择一年期银行定期存款款利率，市场指数收益率我们选择上证指数，深证指数，国债指数分别按40%、30%、30%的权重进行加权平均。 其次，我们按照上文中的方法计算每一期货品种的日间流动性指标，并计算出其均值方差等，考察每个品种的流动性状况，给出按照流动性状况的投资价值排名。 最后，我们综合考虑每个品种的风险收益和市场流动性状况。可以考虑按照不同的比例加权，得出最终的投资价值排序，得到我们需要的结果，形成投资分析报告。
【发表评论】
|
||||||||||||||||||||||||||||||||||||||||||||||||||
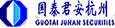
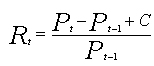，其中C为持有期间现金流入，当持有期间隔比较短时(本文为一天)C值很小，可以忽略不计，这时简单收益率回报就可以写成 
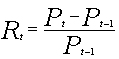。 尽管简单回报含义直观且计算简单，但是它也存在一些缺点，其中最主要的一个问题就有限负债问题。对于一个投资者而言，其最大损失就是他的全部投资，不可能再多，即所谓有限负债。这样，对于投资者而言，最坏的情况就是资产的价格为0，这就意味着未来一期资产回报的变动范围是-100%～无穷大。因此，这种度量方法不能够保证资产价格大于零，而且导致的回报序列不会呈正态分布形式，复杂化了分布形式。为了克服这个不足，我们引入了对数回报度量方法。一个资产的单期对数回报r,定义为单期简单回报R加1后取自然对数，即：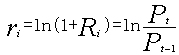 
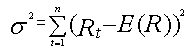
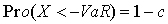
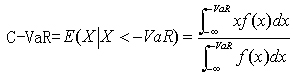
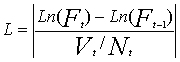
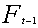是期货前一时刻的收盘价格, 
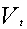是从前一时刻到当前时刻的成交量,
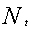是该期货合约当前的持仓量。这个流动性指标的分母是换手率,分子是这段时间的对数收益率。指标的含义是单位合约换手率给价格带来的影响,当换手率一定的时候,价格变化越大,指标值也越大,说明流动性越差；价格变化越小,指标值也越小,流动性就越好。上面对流动性的定义消除了量纲影响,在不同品种之间具备了可比性。此外,由于流动性研究大多采用每日或日内交易数据等高频数据,为了避免在收益率很低时流动性指标的数值会出现相差极大的情况,本文把换手率放在分母中而不是把对数收益率放在分母中,便于数据处理。下面我们就对每个期货品种的日内流动性指标进行计算和分析，考察其流动性状况。最后，结合上文中的风险收益状况综合评价各品种的投资价值。
