|
不支持Flash
|
|
|
|
台湾50股票指数期货市场风险的VaR实证分析(2)http://www.sina.com.cn 2006年12月13日 00:16 中诚期货
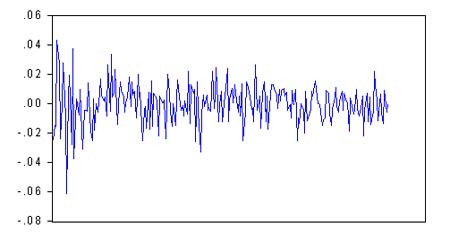
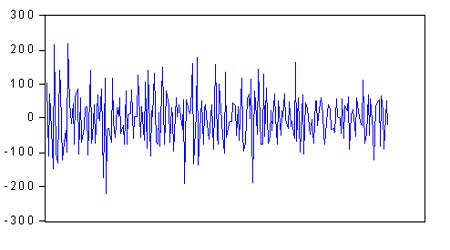
3、异方差性的图形分析 金融资产的价格波动在统计上的体现就是收益的方差,不同时段波动率的大小不同,即说明时间序列具有异方差性。由下图中我们可以看出它们的收益波动程度存在着明显的差异,因此股票期货指数收益和基差变化序列具有异方差性。 图:台湾50股指期货收益率 图:台湾50股指期货基差一阶差分的数据: 4、单位根检验 对台湾50股指期货的收益率及基差一阶差分的进行单位根检验,有表2和标3可以看出,ADF值明显小于1%情况下的t值。所以,至少可以再99%的置信水平下拒绝原假设,序列不存在单位根,是平稳的。 表2:指数期货收益率的单位根检验:
表3:基差波动情况的单位根检验:
模型构建 1、建立 GARCH 模型 为了更准确地度量出它们异方差性,下面对时间序列的异方差性进行模型分析。由于 GARCH 模型能够准确地描述与分析并动态地刻画收益的异方差性,因此选用 ARCH 族模型中的 GARH 模型对各序列进行描述。 GARCH模型的一般表达式可写成: 其中, 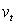 互相独立。一般常假定 为标准正态分布。 互相独立。一般常假定 为标准正态分布。
那么所建立的 GARCH 模型是否很好地刻画了收益的异方差性,有必要对模型进行检验。通常对模型进行拉格朗日乘数检验,其零假设为残差中不再存在 q阶的 ARCH 现象。其残差平方 得到方程可决系数 (n 为观测值个数)在零假设成立时,LM 服从x2(q)分布。如果接受零假设就认为原方程较好地刻画了实际存在的自回归条件异方差,残差中不再存在 ARCH,反之则认为原方程不能反映实际的条件异方差。
运用计量分析软件 Eviews 估计方程和。为找出最优的 GARH模型,我们令 p=1,…,9,q= 0,l,…,9 共做 90 次回归,得到 90 个估计方程组;利用拉格朗日乘数检验的 LM 统汁量,选出最适合的 GARH 模型。对LM 统计量的接受概率越大,则表明残差中存在 ARCH 现象的可能性就越小,因而我们选择接受概率大的 GARCH 模型为最优模型。结果得到股指期货价格指数收益的 GARCH(2,1)为最优模型。 表4:ARCH Test:
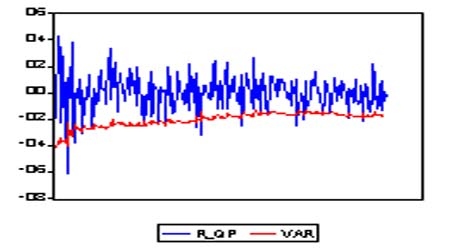
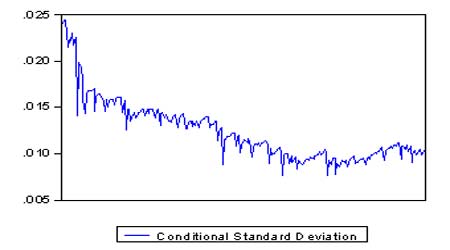
期货指数收益序列的36阶ARCH—LM检验,证实股指期货收益率序列具有GARCH效应。 对于GARCH(2,1)模型形势如下: 在条件方差等式中,系数 2、股指期货指数收益的VaR 值的计算 在了解了股票期货指数收益的分布特性、波动特性之后,我们就可以根据它们的这些特性计算其 VaR 值。本文采用方法为基于 GARH 模型的计算方法。 VaR估计的条件方差方法属于动态VaR计算的分析方法,由于实际金融市场中收益率的厚尾性会导致VaR对风险的低估,因此可以利用GARCH模型类中的条件方差来度量股票市场VaR。这样,VaR 首先利用期货指数收益的 GARCH(2,1)模型计算条件方差,计算出条件方差,开方后得到条件标准差,将计算得到的各期的条件标准差代入式(1),得到在 95%置信度下期货指数收益的 VaR 值。经计算得出期货指数收益的 GARCH(2,1)模型的条件标准差和 VaR 值。 期货价格指数收益与 VaR 值的比较图 在95%和99% 置信区间下计算的每日VaR比例与期货每日损失的比较
【发表评论】
|
不支持Flash
不支持Flash
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
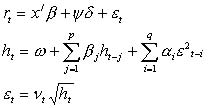
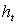 为条件方差,
为条件方差, 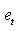 进行回归如下:
进行回归如下: 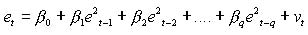
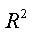 ,则 LM 统计量为:
,则 LM 统计量为: 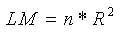
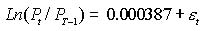
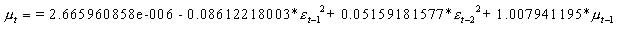
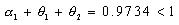 ,满足参数约束条件。主模式中,变量
,满足参数约束条件。主模式中,变量  的系数估计值近似为1,表明是单位根过程。模型的AIC 和SC值都比较小,都接近-6,可以认为该模型较好的拟合了数据。
的系数估计值近似为1,表明是单位根过程。模型的AIC 和SC值都比较小,都接近-6,可以认为该模型较好的拟合了数据。
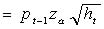 ,其中 是由GARCH模型估计得到的条件方差,
,其中 是由GARCH模型估计得到的条件方差, 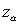 根据收益率分布决定。
根据收益率分布决定。