基于协整的股指期货跨期套利策略
◇ 中金所宣布沪深300股指期货合约将于2010年4 月16日正式上市交易
■ 与传统定价方法相比,我们的跨期套利策略得到了更好的套利效果
对同样的样本数据,传统方法的spread一直处于无套利空间,一次套利机会都没有,而基于我们的模型在两个交易日内跨期套利次数为18次,成功率100%,投入资金成本2200万韩元,总收益约80万韩元,收益率3.63%,明显优于基于成本理论的套利效果。由此可见,基于GARCH模型的跨期套利策略大大提高了同时段套利机会的次数和效率。
■ 传统股指期货跨期套利方法的缺陷
传统的股指期货跨期套利方法是基于持有成本理论,而持有成本理论中的股息收益率 不易确定, 限制了其应用,再者基于持有成本理论的套利往往需要经历较长时间才能完成, 因为它的价差会一直处于偏高或偏低的状态,只有在合约临近到期时才有回归的压力。
■ 我们的股指期货跨期套利策略
我们利用样本内和样本外两组数据,以样本内数据建立模型,同时假设样本内方差resid01和样本外方差resid02有相同的分布,且都有向零均值回归的要求。随后根据GARCH(1,1)得到resid02的时变方差,再根据resid02和resid02的时变方差制定相应的策略。从实证结果看,套利交易次数占全部交易日的比例在20%以上,单次套利交易的平均收益约为45000韩元,以单次套利投入资金2200万韩元计算,单次套利交易的收益率约0.2%。
■ 我们策略可能存在的问题
在我们策略模型中的 并不为一整数,而在现实交易中只能做整数合约的交易,那将需要将多余的非整数部分用ETF或成份股的组合来对冲。
1. 研究内容及意义
股指期货的两个不同期货合约因为对应的同一个股票指数,所以存在着长期协整关系的基础。依据配对交易的思想,基于协整的股指期货套利的核心在于准确发现价差交易出现的时机和概率,而本文应用协整方法来构建不同到期月份合约价格序列的长期均衡关系,估计价差序列的分布,从而制定恰当的价差交易策略。
2. 研究成果综述
N.Burgess(1999)利用协整模型对FTSE 100指数进行套利取得了良好的效果,Board和Sutcliffe(1996)利用协整方法对大阪、新加坡和芝加哥的日经225指数合约之间的价差套利研究表明也存在套利交易空间。同时陈守东等(2003)和仲黎明等(2003)利用协整分析了在股票指数间的长期平稳关系或引导关系。但是上述文献都没有涉及到股指期货跨期套利的研究,而国内的股指期货跨期套利研究则基本上停留在文字描述或基于持有成本定价理论的无套利价差空间的分析,而这些方法存在着股息收益率不易确定、套利周期长,风险难控等方面的缺点。
3. 跨期套利的定义与传统定价方法
股指期货跨期套利即为在同一交易所进行同一指数但不同交割月份的套利活动。对于同一个标的资产,交易所会设计出不同交割月份的期货合约,不同交割月份的股指期货合约理论价格可以表示为:
其中: 表示股指期货的时间 时的价格; 表示现货指数在时间 时的价格, 表示以连续复利计算的无风险利率; 表示股息收益率; 表示期货合约到期时间(年); 表示现在的时间(年)。
在假设无风险利率和股息率相同的情况下,任意两张合约之间的理论价格可以表示为:

由此可以得到两张期货合约之间的价格关系为:

4. 基于协整的跨期套利模型
传统的股指期货跨期套利方法有如下缺陷:
1) 基于持有成本理论中的股息收益率 不易确定, 限制了其应用;
2) 基于持有成本理论的套利往往需要经历较长时间才能完成, 因为它的价差会一直处于偏高或偏低的状态,只有在合约临近到期时才有回归的压力。
而基于协整的跨期套利模型则可以避免上面的缺陷,并且可以充分利用已有的市场交易数据所提供的最新信息, 从而发现更多的套利机会。其基本思路如下:
将近期合约 和远期合约 的数据分为样本内与样本外数据两部分,对样本内数据建立模型,样本外数据以样本内数据建立的模型为依据进行研究。

通过ARCH LM检验,可以知道残差resid01自身的方差并非恒定不变,类似于其他金融时间序列,resid01自身的方差也是存在时变的特性,对resid01序列尽量合理的建模是提高交易效率的有效手段。我们利用样本内和样本外两组数据,以样本内数据建立模型,同时假设样本内方差resid01和样本外方差resid02有相同的分布,且都有向零均值回归的要求。随后根据GARCH(1,1)得到resid02的时变方差,求得:
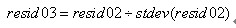
再根据resid03制定相应的策略。
5. 模型的运行过程与结果
5.1 研究样本
本文选取韩国KOSPI200股指期货进行实证研究。数据为KMH9与KMM9两个合约在09-3-5到09-3-6时间段内的1MIN高频数据。我们将1-500的数据做为样本内数据,建立模型,当存在协整关系时,对样本外501-607数据以这一协整模型的结果为依据进行跨期套利交易的研究。
图表1 KOSPI200指数期货合约说明
| 项目 | 说明 |
| 标的指数 | KOSPI200 |
| 交易单位 | 1张合约 |
| 乘数 | 500000韩元 |
| 最小变动值 | 0.05点,相当于25000韩元 |
| 合约月份 | 3月、6月、9月、12月 |
| 交易时间 | 周一到周五:09:00-15:15 最后交易日:09:00-14:50 |
| 最后交易日 | 合约月份的第二个星期四 |
| 最后交割日 | 最后交易日的次日 |
| 头寸限制 | 净头寸5000张 |
| 交割方法 | 现金交割 |
资料来源:光大证券研究所
5.2 描述性统计与相关性检验
图表2 ln(kmh9)和ln(kmm9)的走势图
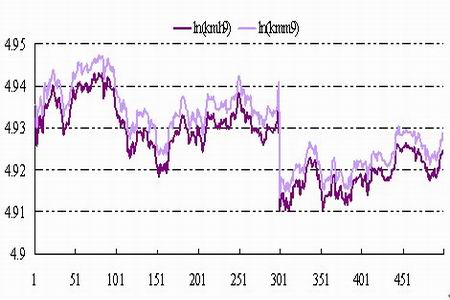
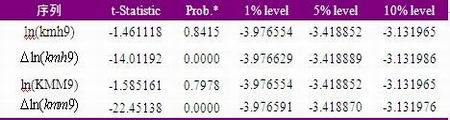
从ln(kmh9)和ln(kmm9)图形中可以看出两者均含有常数项。对ln(kmh9)和ln(kmm9)进行单位根检验,检验结果显示,ln(kmh9)和ln(kmm9)原序列存在单位根,而其一阶差分在1%的显著性水平下拒绝原假设,接受不存在单位根的备择假设,因此两者都是 I(1)序列,可能存在协整关系。
资料来源:光大证券研究所
随后,对ln(kmh9)和ln(kmm9)做一元线性回归,模型残差resid01的单位根检验结果如表所示:
| t-Statistic | Prob.* | ||
| Augmented Dickey-Fuller test statistic | -22.58282 | 0.0000 | |
| Test critical values | 1% level | -2.569604 | |
| 5% level | -1.941459 | ||
| 10% level | -1.616273 | ||
资料来源:光大证券研究所
由上表知,resid01不含有单位根,是稳定序列,从而可以认为ln(kmh9)和ln(kmm9)序列之间确实存在协整关系。
新浪声明:新浪网登载此文出于传递更多信息之目的,并不意味着赞同其观点或证实其描述。文章内容仅供参考,不构成投资建议。投资者据此操作,风险自担。