来源:原点阅读
编辑:云开叶落
考届一直流传着这样一个传说,“不会就选C”据说被历代学子们奉为不会做题时答题“上策”。
你有没在考试中遇到选择题拿不准答案就选了C,然后就蒙对了的经历?

标准化考试是国际上广为流行的考试方法,它具有客观性强,覆盖面广,评卷迅速等优点。选择题是标准化考试中最常采用的题型,我们在各种考试中都经常能见到选择题的身影。
从题目的结构看,一般分为两部分:一部分是提出或陈述一个问题,另一部分是备选答案,包含一个正确答案及几个错误答案。我们来看下面的例子:
[选择题]以下图形中有几个是正方体的表面展开图?
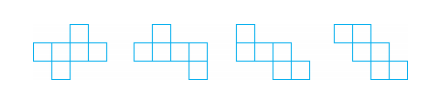
A.1个;B.2个;C.3个;D.4个。例子中备选答案有4个,只有D项是正确的。
一道选择题的备选答案数,我们称为“项数”。上面的例是一道4项选择题。虽然选择题作为考试的题型,有着许多优点,但也存在一个严重的不足,即难于摒弃“碰运气”的成分。具体地说,对一个一无所知的人来说,单凭机遇也可能碰上几个正确的答案。
事实上,一道λ项的选择题,随机选取恰好碰上正确答案的概率是1/λ,碰到不正确答案的概率是1-(1/λ)。假设共有n 道这样的选择题,光凭机遇随机选对k题的概率为
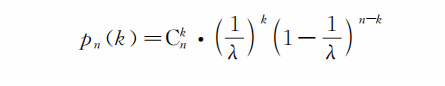
具体些,如果我们有10道题,每道题有4个备选答案,即 n=10,λ=4。
那么,可以一个个算出随机选对k题的概率(只是相应的
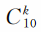
要从杨辉三角的第10排去查),列表如下。
随机选题概率
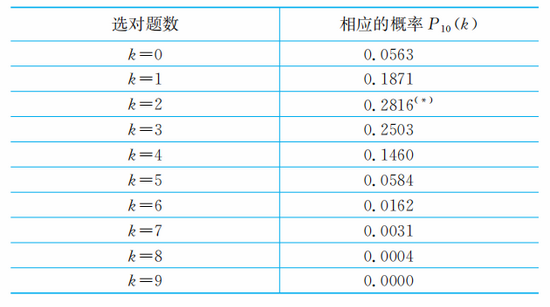
从表中容易看出,光凭机遇选对两道题或三道题的可能性占了过半,如果这也“给分”的话,显然是不够合理的。正是由于存在这种不合理性,所以许多国家的考试组织者,都对各种考试做了形式各异的弥补性规定。
如美国中学数学竞赛,共有30道选择题,每卷给30分基本分,以平衡随机得分。只有全错才得0分, 但全错的可能性是极少的。
又如我国有些数学联赛试题,对选择题得分做如下规定:答对得满分,答错得0分, 不答得1分。这主要是鼓励学生“知之为知之,不知为不知”,不要去做碰运气选题的事。再如2013年苏州大学的自主招生,语文、数学、物理、化学的考试试题均由40道选择题组成,得分规定为:选对的得5分;不选的得0分;选错的扣2分。这里设置的扣分,意在惩罚那些碰运气的人。
上面的众多规定,既有合理的一面,也都有不合理的地方。从科学的角度看,要让那些靠碰运气选题的人得不到分,才算合理。为此,我们必须去求靠碰运气最可能会选对的题数k* ,这相当于解以下不等式组:
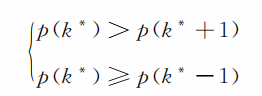
仅限于初中的知识,要解上面不等式组还有一定困难,但解得的结果却是很简单的:
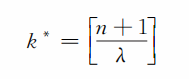
其中[x]表示不超过x 的最大整数。如[π]=3,[lg32]=1等。在前面例中
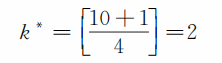
这与表中查到的相应概率的最大值是一致的。当k* 确定之后,我们便可以设置扣分,使得选对k* 题的人得不到分。科学的扣分法有两种。
第一种方法:
设答对一道题得r分,答错一道题得0分,每卷以-k*r为基本分,且总得分不取负值。显然,全对者得(n-k* )r,即为满分。如前例中的10道题,假定每道题答对得5分,由于k* =2,所以基本分可定为-2×5=-10分,满分为40分。
第二种方法:
设答对一道题得r分,答错一道题扣t分,基本分为0分。t的选取,要使选对k* 题的人得不到分数(因为我们认为他是纯粹靠运气选对的)。因此,该卷所得分数应与所扣分数相当, 即k*r=(n-k* )t,算得
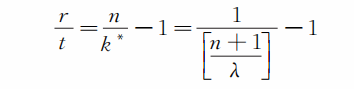
对于多项选择题,随着项数λ 的增大,靠机遇选对的题数 k* 相应减少。对于这种情形,即使不设置扣分,也不至于对总分造成过大的影响。
从k* 的计算式可以看出,要减少k* 的途径有两条,一是减少题目数量,二是增大项数。减少题目的数量是没有实际意义的,而增大备选答案的个数,又对设计题目造成了困难。怎么办呢?最近,有的考试采用了一种叫作“多解选择”的办法,每个备选答案都可能是正确的或错误的(与单一选择的区别是,不再只有一个答案正确)。这样,λ 个备选答案,每个答案都有“取”与“不取”两种选择,共有
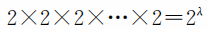
种选取的方法。除去都不选的一种情形,实际项数有

这显然比单一选项的项数要高得多。例如,备选答案只有3个的多解选择,实际项数
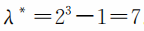
项数这样高,随机选对的可能性势必很小。因而,多解选择一般是没有必要去设置扣分的。

“掌”握科技鲜闻 (微信搜索techsina或扫描左侧二维码关注)

















